参考解答
正确答案:B=ATA=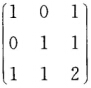 的特征值对应的特征向量依次为
的特征值对应的特征向量依次为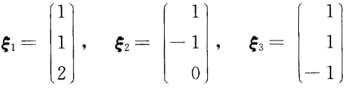 于是可得rank A=2
于是可得rank A=2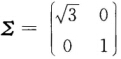 且有正交矩阵
且有正交矩阵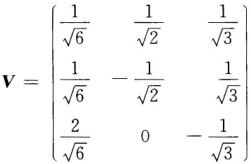 计算得到
计算得到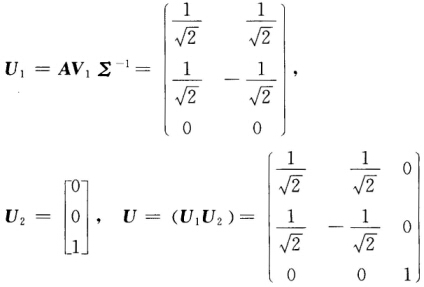 则A的奇异值分解为
则A的奇异值分解为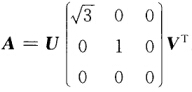 总结A的奇异值分解的步骤如下: (1)计算AHA求AHA的n个特征值λi及A的正奇异值σi=
总结A的奇异值分解的步骤如下: (1)计算AHA求AHA的n个特征值λi及A的正奇异值σi=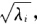 i=12…γ. (2)求AHA的n个特征向量并用正交化方法化为标准正交向量ε1ε2…εn它们构成酉矩阵V=(ε1ε2…εrεr+1…εn). (3)取V1=(ε1ε2…εr)∑1=diag(σ1σ2…σn)并计算 U1=AV1∑1-1(U1的γ个列正交). (4)在Cm中取与U1的列向量正交的m-γ个标准正交向量组成U2使得(U1U2)=U为酉矩阵从而求得U则
i=12…γ. (2)求AHA的n个特征向量并用正交化方法化为标准正交向量ε1ε2…εn它们构成酉矩阵V=(ε1ε2…εrεr+1…εn). (3)取V1=(ε1ε2…εr)∑1=diag(σ1σ2…σn)并计算 U1=AV1∑1-1(U1的γ个列正交). (4)在Cm中取与U1的列向量正交的m-γ个标准正交向量组成U2使得(U1U2)=U为酉矩阵从而求得U则
B=ATA=的特征值对应的特征向量依次为于是可得rankA=2,,且有正交矩阵计算得到则A的奇异值分解为总结A的奇异值分解的步骤如下:(1)计算AHA,求AHA的n个特征值λi及A的正奇异值σi=,i=1,2,…,γ.(2)求AHA的n个特征向量,并用正交化方法化为标准正交向量ε1,ε2,…,εn,它们构成酉矩阵V=(ε1,ε2,…,εr,εr+1,…,εn).(3)取V1=(ε1,ε2,…,εr),∑1=diag(σ1,σ2,…,σn),并计算U1=AV1∑1-1(U1的γ个列正交).(4)在Cm中,取与U1的列向量正交的m-γ个标准正交向量组成U2,使得(U1U2)=U为酉矩阵,从而求得U,则
相似问题
若∥.∥是算子范数 则 (1)∥E∥=1; (2)∥A-1∥≥∥A∥-1; (3)请帮忙给出正确答案
若∥ ∥是算子范数,则 (1)∥E∥=1; (2)∥A-1∥≥∥A∥-1; (3)请帮忙给出正确答案和分析,谢谢!
设∥A∥v ∥A∥μ是对应于两个向量范数∥x∥v ∥x∥μ=∥Bx∥v的算子范数 B可逆 则∥A∥μ
设∥A∥v,∥A∥μ是对应于两个向量范数∥x∥v,∥x∥μ=∥Bx∥v的算子范数,B可逆,则∥A∥μ=∥BAB-1∥v请帮忙给出正确答案和分析,谢谢!
证明:0m×n的自反广义逆矩阵仅为0n×m.请帮忙给出正确答案和分析 谢谢!
证明:0m×n的自反广义逆矩阵仅为0n×m.请帮忙给出正确答案和分析,谢谢!
设矩阵级数收敛(绝对收敛) 证明也收敛(绝对收敛) 且其中A(k) ∈Cm×n P∈Cs×m Q
设矩阵级数收敛(绝对收敛),证明也收敛(绝对收敛),且其中A(k) ∈Cm×n ,P∈Cs×m,Q ∈Cn×l请帮忙给出正确答案和分析,谢谢!
设A是n×n的实对称矩阵 并且A2=0 问能用几种方法证明A=0.请帮忙给出正确答案和分析 谢谢!
设A是n×n的实对称矩阵,并且A2=0,问能用几种方法证明A=0.请帮忙给出正确答案和分析,谢谢!


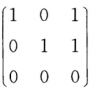 的奇异值分解.
的奇异值分解.









