参考解答
正确答案:若Ak→0设λ为A的任意特征值x≠0是满足Ax=λx的特征向量仅当∣λ∣<1时才有AkX=λxk→0.由λ的任意性有γ(A)<1.反过来如果γ(A)<1则存在某个矩阵范数∥.∥使得∥A∥<1.又由于当k→∞时有∥Ak∥≤∥A∥k→0因此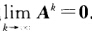
若Ak→0,设λ为A的任意特征值,x≠0是满足Ax=λx的特征向量,仅当∣λ∣<1时才有AkX=λxk→0.由λ的任意性,有γ(A)<1.反过来,如果γ(A)<1,则存在某个矩阵范数∥.∥,使得∥A∥<1.又由于当k→∞时,有∥Ak∥≤∥A∥k→0,因此
相似问题
若A和B是任意两个m×n矩阵 则AHA=BHB当且仅当存在一个m×n酉矩阵Q 使得QA=B.请帮忙给
若A和B是任意两个m×n矩阵,则AHA=BHB当且仅当存在一个m×n酉矩阵Q,使得QA=B.请帮忙给出正确答案和分析,谢谢!
设A是正规矩阵 证明: (1)A的特征向量也是AH的特征向量; (2)AX与AHX的长度相等.请帮忙
设A是正规矩阵,证明: (1)A的特征向量也是AH的特征向量; (2)AX与AHX的长度相等.请帮忙给出正确答案和分析,谢谢!
设∥x∥是Pn中的向量范数 A∈Pn×n 则∥Ax∥也是Pn中的向量范数的充要条件为A是可逆矩阵.请
设∥x∥是Pn中的向量范数,A∈Pn×n,则∥Ax∥也是Pn中的向量范数的充要条件为A是可逆矩阵.请帮忙给出正确答案和分析,谢谢!
证明:方程组AHAx=AHb是相容的 其中A∈Cm×n b∈Cm.请帮忙给出正确答案和分析 谢谢!
证明:方程组AHAx=AHb是相容的,其中A∈Cm×n,b∈Cm.请帮忙给出正确答案和分析,谢谢!
设A2=A=AH 试证明:A=A+.请帮忙给出正确答案和分析 谢谢!
设A2=A=AH,试证明:A=A+.请帮忙给出正确答案和分析,谢谢!


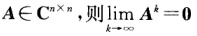 当且仅当γ(A)<1.
当且仅当γ(A)<1.









