证明：马鞍面M：z=xy为直纹面 但不是可展曲面 其参数表示为x(u v)=(u v uv)．请帮忙
证明：马鞍面M：z=xy为直纹面，但不是可展曲面，其参数表示为x(u，v)=(u，v，uv)．
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***102
2024-11-16 22:40:57
正确答案：因为固定u时x(uv)=a(u)+vl(u)=(u00)+v(01u)是过点a(u)、以l(u)为方向的直线故M为直纹面．又因为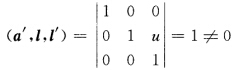
故根据定理2．2．1M不是可展曲面．
因为固定u时,x(u,v)=a(u)+vl(u)=(u,0,0)+v(0,1,u)是过点a(u)、以l(u)为方向的直线,故M为直纹面．又因为故根据定理2．2．1,M不是可展曲面．
相似问题
证明：圆柱螺线ρ(v)=(acosv asinv bv) (a>0 b>0)的主法线曲面M是正螺面
证明：圆柱螺线ρ(v)=(acosv，asinv，bv) (a>0， b>0)的主法线曲面M是正螺面x(u，v)=(ucosv，usinv，bv)，它不是可展曲面．请帮忙给出正确答案和分析，谢谢！
求曲面F(x y z)=0的曲率线．请帮忙给出正确答案和分析 谢谢！
求曲面F(x，y，z)=0的曲率线．请帮忙给出正确答案和分析，谢谢！
对R3中定向光滑的2维闭曲面M 如果(Minkowski公式)设MCR3为2维光滑 定向 紧致曲面
对R3中定向光滑的2维闭曲面M，如果(Minkowski公式)设MCR3为2维光滑、定向、紧致曲面，x(P)为它的位置(Minkowski公式)设MCR3为2维光滑、定向、紧致曲面，x
证明：双益抛物线(马鞍面)M：x(u v)=(a(u+v) b(u一v) 2uv) (a>0 b>0
证明：双益抛物线(马鞍面)M：x(u，v)=(a(u+v)，b(u一v)，2uv) (a>0，b>0)不是可展曲面．请帮忙给出正确答案和分析，谢谢！
设曲面M的第1基本形式取等温形式：I=ρ2(du2+dv2)．证明：其中从而 当一时 KG=4c(常
设曲面M的第1基本形式取等温形式：I=ρ2(du2+dv2)．证明：其中从而，当一时，KG=4c(常数)．请帮忙给出正确答案和分析，谢谢！
