证明：负常Gauss(总)曲率曲面在平面上取极坐标系{r θ}．(1)证明：I=dr2＋r2dθ2；
证明：负常Gauss(总)曲率曲面在平面上取极坐标系{r，θ}．(1)证明：I=dr2＋r2dθ2；(2)计算rijk．
在平面上取极坐标系{r，θ}．(1)证明：I=dr2+r2dθ2；(2)计算rijk．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***102
2024-11-17 00:45:35
正确答案：(1)(参阅习题2．8．20)x(rθ)=(rcosθrsinθ)．计算得xr'=(cosθsinθ)xθ'=(一rsinθrcosθ)E=xr'.xr'=1 F=xr'.xθ'=0G=xθ'.xθ'=r2I=dr2+r2dθ2．(2)因F=0即xr'⊥xθ'E=1G=r2所以根据例2．4．1得到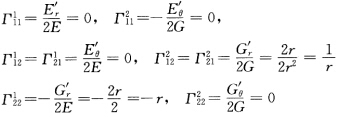
(1)(参阅习题2．8．20)x(r,θ)=(rcosθ,rsinθ)．计算得xr'=(cosθ,sinθ),xθ'=(一rsinθ,rcosθ),E=xr'.xr'=1,F=xr'.xθ'=0,G=xθ'.xθ'=r2,I=dr2+r2dθ2．(2)因F=0,即xr'⊥xθ',E=1,G=r2,所以根据例2．4．1,得到
相似问题
设曲面M：x(u v)=(ucosv usinv lnu)与设常Gauss曲率曲面M：x(u v)的
设曲面M：x(u，v)=(ucosv，usinv，lnu)与设常Gauss曲率曲面M：x(u，v)的第1基本形式为 ．曲面 证明：与M设常Gauss曲率曲面M：x(u，v)的第1基本形式为
证明：每一条曲线C：x(s)在它的主法线曲面上是渐近曲线．请帮忙给出正确答案和分析 谢谢！
证明：每一条曲线C：x(s)在它的主法线曲面上是渐近曲线．请帮忙给出正确答案和分析，谢谢！
证明：连通曲面为球面片或平面片请帮忙给出正确答案和分析 谢谢！
证明：连通曲面为球面片或平面片请帮忙给出正确答案和分析，谢谢！
R3中k≠0 τ≠0的C4连通曲线x(s)为球面曲线等价于如果x(s)为球面曲线 则如果x(s)为球
R3中k≠0，τ≠0的C4连通曲线x(s)为球面曲线等价于如果x(s)为球面曲线，则如果x(s)为球面曲线，则请帮忙给出正确答案和分析，谢谢！
求球面x(θ φ)=(Rsinθcosφ Rsin θsinφ Rcosθ)的第1 第2基本形式以及
求球面x(θ，φ)=(Rsinθcosφ，Rsin θsinφ，Rcosθ)的第1、第2基本形式以及Gauss曲率KG、平均曲率H．请帮忙给出正确答案和分析，谢谢！
