求悬链面M：求双曲抛物面M：x(u v)=(a(u＋v) b(u一v)2uv) (a>0 b>0)(
求悬链面M：求双曲抛物面M：x(u,v)=(a(u＋v),b(u一v)2uv) (a>0，b>0)(它的直角坐标方程为的渐
求双曲抛物面M：x(u,v)=(a(u+v),b(u一v)2uv) (a>0，b>0)(它的直角坐标方程为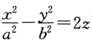
的渐近曲线．
请帮忙给出正确答案和分析，谢谢！
参考解答
473***102
2024-11-17 00:56:00
正确答案：计算得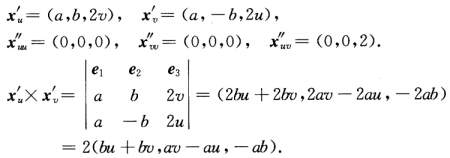
单位法向量为
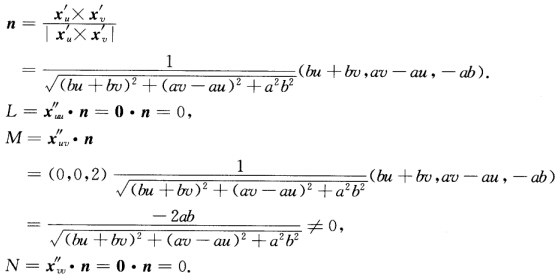这表明LMN不全为0．因此渐近方程Ldu2+2Mdudv+Ndv2=0至多有2个解．事实上该方程为2Mdudv=0.du2+2Mdudv+0.dv2=Ldu2+2Mdudv+Ndv2=0 即dudv=0．于是渐近曲线恰为两族坐标曲线u=u0(常数)及v=v0(常数)它就是双曲线抛物面M上的两族直线．
计算得单位法向量为这表明L,M,N不全为0．因此,渐近方程Ldu2+2Mdudv+Ndv2=0至多有2个解．事实上,该方程为2Mdudv=0.du2+2Mdudv+0.dv2=Ldu2+2Mdudv+Ndv2=0,即dudv=0．于是,渐近曲线恰为两族坐标曲线u=u0(常数)及v=v0(常数),它就是双曲线抛物面M上的两族直线．
相似问题
证明：负常Gauss(总)曲率曲面在平面上取极坐标系{r θ}．(1)证明：I=dr2＋r2dθ2；
证明：负常Gauss(总)曲率曲面在平面上取极坐标系{r，θ}．(1)证明：I=dr2＋r2dθ2；(2)计算rijk．在平面上取极坐标系{r，θ}．(1)证明：I=dr2+r2dθ2；(2
设曲面M：x(u v)=(ucosv usinv lnu)与设常Gauss曲率曲面M：x(u v)的
设曲面M：x(u，v)=(ucosv，usinv，lnu)与设常Gauss曲率曲面M：x(u，v)的第1基本形式为 ．曲面 证明：与M设常Gauss曲率曲面M：x(u，v)的第1基本形式为
证明：每一条曲线C：x(s)在它的主法线曲面上是渐近曲线．请帮忙给出正确答案和分析 谢谢！
证明：每一条曲线C：x(s)在它的主法线曲面上是渐近曲线．请帮忙给出正确答案和分析，谢谢！
证明：连通曲面为球面片或平面片请帮忙给出正确答案和分析 谢谢！
证明：连通曲面为球面片或平面片请帮忙给出正确答案和分析，谢谢！
R3中k≠0 τ≠0的C4连通曲线x(s)为球面曲线等价于如果x(s)为球面曲线 则如果x(s)为球
R3中k≠0，τ≠0的C4连通曲线x(s)为球面曲线等价于如果x(s)为球面曲线，则如果x(s)为球面曲线，则请帮忙给出正确答案和分析，谢谢！
