R3中k≠0 τ≠0的C4连通曲线x(s)为球面曲线等价于如果x(s)为球面曲线 则如果x(s)为球
R3中k≠0，τ≠0的C4连通曲线x(s)为球面曲线等价于如果x(s)为球面曲线，则
如果x(s)为球面曲线，则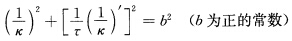
请帮忙给出正确答案和分析，谢谢！
参考解答
473***102
2024-11-17 00:47:21
正确答案：证法1 根据习题1．3．21的证明对球面曲线x(s)有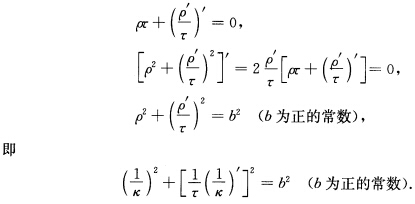
证法2根据习题1．3．22证法2对球面曲线x(s)有
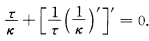因为曲线x(s)的密切球面中心为
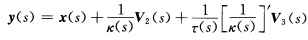所以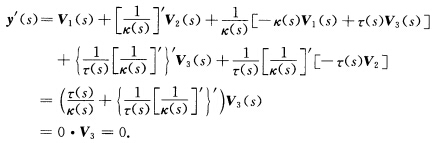
积分得y(s)=y0(常向量)．故密切球面半径b(s)的平方
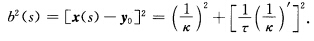因为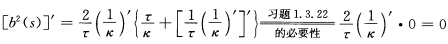
故b2(s)为常数而b(s)=b为正的常数．
证法1根据习题1．3．21的证明,对球面曲线x(s),有证法2根据习题1．3．22证法2,对球面曲线x(s),有因为曲线x(s)的密切球面中心为所以积分得y(s)=y0(常向量)．故密切球面半径b(s)的平方因为故b2(s)为常数,而b(s)=b为正的常数．
相似问题
求球面x(θ φ)=(Rsinθcosφ Rsin θsinφ Rcosθ)的第1 第2基本形式以及
求球面x(θ，φ)=(Rsinθcosφ，Rsin θsinφ，Rcosθ)的第1、第2基本形式以及Gauss曲率KG、平均曲率H．请帮忙给出正确答案和分析，谢谢！
证明：曲面M：x(x y)=(x y f(x y))的第1 第2基本形式分别为从原点O向z=R处的切
证明：曲面M：x(x，y)=(x，y，f(x，y))的第1、第2基本形式分别为从原点O向z=R处的切平面作中心投影．证明从原点O向z=R处的切平面作中心投影．证明：球面M
若一条测地线与u线的交角为θ 证明：请帮忙给出正确答案和分析 谢谢！
若一条测地线与u线的交角为θ，证明：请帮忙给出正确答案和分析，谢谢！
X=(x 一y)；请帮忙给出正确答案和分析 谢谢！
X=(x，一y)；请帮忙给出正确答案和分析，谢谢！
设一条曲率线(非渐近曲线)C的密切平面与曲面的切平面交于定角 则该曲率线必为平面曲线．请帮忙给出正确
设一条曲率线(非渐近曲线)C的密切平面与曲面的切平面交于定角，则该曲率线必为平面曲线．请帮忙给出正确答案和分析，谢谢！
