求球面x(θ φ)=(Rsinθcosφ Rsin θsinφ Rcosθ)的第1 第2基本形式以及

正确答案：解法1x_θ^'=(Rcos θcosφRcos θsinφ-Rsinθ)x_φ^'=(-RsinθsinφRsin θcosφ0)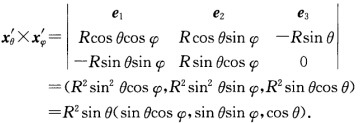单位法向量为x_φφ^''=(-Rsinθcosφ-Rsinθsinφ0)．于是E=x_θ^'．x_θ^'=R²F=x_θ^'.x_φ^'=0(x_θ^'⊥x_φ^')G=x_φ^'.x_φ^'=R²sin²θL=x_θθ^''.n=一RM=x_θφ^''.n=0N=x_φφ^''.n=一Rsin²θ．球面的第1和第2基本形式分别为I=ds²=Edθ²+2Fdθdφ+Gdφ²=R²dφ²+R²sin²θdφ²Ⅱ=Ldθ²+2Mdθdφ+Ndφ²=一Rdθ²-Rsin²θdφ²．根据注2．6．1有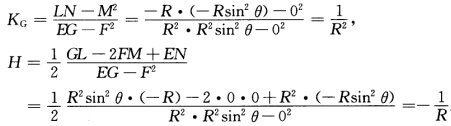解法2从球面作为例2．6．3的特例得到上述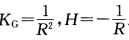解根据习题2．6．3的结果有：(1)x(uv)=(sin vcosvsin vsinucosv)；(2)x(uv)=(一sin ucosv一sin usinv一cosv)．
解法1xθ'=(Rcosθcosφ,Rcosθsinφ,-Rsinθ),xφ'=(-Rsinθsinφ,Rsinθcosφ,0),单位法向量为xφφ''=(-Rsinθcosφ,-Rsinθsinφ,0)．于是E=xθ'．xθ'=R2,F=xθ'.xφ'=0(xθ'⊥xφ'),G=xφ'.xφ'=R2sin2θ,L=xθθ''.n=一R,M=xθφ''.n=0,N=xφφ''.n=一Rsin2θ．球面的第1和第2基本形式分别为I=ds2=Edθ2+2Fdθdφ+Gdφ2=R2dφ2+R2sin2θdφ2,Ⅱ=Ldθ2+2Mdθdφ+Ndφ2=一Rdθ2-Rsin2θdφ2．根据注2．6．1,有解法2从球面作为例2．6．3的特例得到上述解根据习题2．6．3的结果,有：(1)x(u,v)=(sinvcosv,sinvsinu,cosv)；(2)x(u,v)=(一sinucosv,一sinusinv,一cosv)．