设A是n阶实对称矩阵 且A2=E.证明:存在正交矩阵Q 使得请帮忙给出正确答案和分析 谢谢!
设A是n阶实对称矩阵,且A2=E.证明:存在正交矩阵Q,使得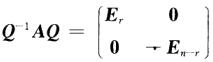
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:法1 因为A是n阶实对称矩阵所以存在n阶矩阵T使得T-1AT=diag(λ1λ2…λn)其中λ1λ2…λn为A的n个特征值(重根按重数列出).于是T-1A2T=T-1ATT-1AT=diag(λ1λ2…λn).diag(λ1λ2…λn)=diag(λ12λ22…λn2).又因为A2=E所以E=T-1ET=T-1A2T=diag(λ12λ22…λn2).因此有λi=±1(i=12…n).不妨设λi=1的重数为r则λi=-1的重数为n-r.只要通过置换将λi=1集中排列在前面则有正交矩阵Q使得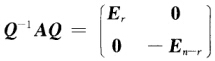 法2 因为A是n阶实对称矩阵且A2=E若令g(x)=x2-1则g(x)为A的零多项式且无重根故A相似于对角矩阵.设λ为A的任一特征值则λ=±1.不妨设λi=-1的重数为n-r.只要将λi=1集中排列在前面则有正交矩阵Q使得
法2 因为A是n阶实对称矩阵且A2=E若令g(x)=x2-1则g(x)为A的零多项式且无重根故A相似于对角矩阵.设λ为A的任一特征值则λ=±1.不妨设λi=-1的重数为n-r.只要将λi=1集中排列在前面则有正交矩阵Q使得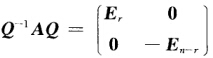
法1因为A是n阶实对称矩阵,所以存在,n阶矩阵T,使得T-1AT=diag(λ1,λ2,…,λn),其中λ1,λ2,…,λn为A的n个特征值(重根按重数列出).于是T-1A2T=T-1ATT-1AT=diag(λ1,λ2,…,λn).diag(λ1,λ2,…,λn)=diag(λ12,λ22,…,λn2).又因为A2=E,所以E=T-1ET=T-1A2T=diag(λ12,λ22,…,λn2).因此有λi=±1(i=1,2,…,n).不妨设λi=1的重数为r,则λi=-1的重数为n-r.只要通过置换将λi=1集中排列在前面,则有正交矩阵Q,使得法2因为A是n阶实对称矩阵,且A2=E,若令g(x)=x2-1,则g(x)为A的零多项式,且无重根,故A相似于对角矩阵.设λ为A的任一特征值,则λ=±1.不妨设λi=-1的重数为n-r.只要将λi=1集中排列在前面,则有正交矩阵Q,使得
相似问题
设ξ η是相互独立的 且概率密度分别为盒中装有大小相同的球10个 编号为0 1 2 … 9 从中任取
设ξ,η是相互独立的,且概率密度分别为盒中装有大小相同的球10个,编号为0,1,2,…,9,从中任取了1个,盒中装有大小相同的球10个,编号为0,1,2,
设ξ η是相互独立的 且概率密度分别为设某运动员投篮命中的概率为0.6 求他一次投篮时 投篮命中次设
设ξ,η是相互独立的,且概率密度分别为设某运动员投篮命中的概率为0.6,求他一次投篮时,投篮命中次设某运动员投篮命中的概率为0.6,求他一次投篮时
设随机变量X和Y相互独立均服从N(0 42) 而X1 X2 … X15和Y1 Y2 … Y16分别来
设随机变量X和Y相互独立均服从N(0,42),而X1,X2,…,X15和Y1,Y2,…,Y16分别来自总体X和Y的样本,求统计量服从的分布及其自由度.请帮忙给出正确答
设总体X~N(μ σ2) X1 X2 … Xn为来自总体X的样本 当用有一批枪弹 其初速度V~N(μ
设总体X~N(μ,σ2),X1,X2,…,Xn为来自总体X的样本,当用有一批枪弹,其初速度V~N(μ,σ2),其中μ=950,σ=1有一批枪弹,其初速度V~N(μ,σ2)
设X1 X2 X3 X4是来自正态总体N(0 32)的简单随机样本 若随机变量X=a(X2一3X2
设X1,X2, X3,X4是来自正态总体N(0,32)的简单随机样本,若随机变量X=a(X2一3X2)2+b(2X3—5X4)2,试求a,b的值,使统计量X服从χ2分布,并求其自由度.












