设A(k)∈Cm×n B(k)∈Cn×l 证明请帮忙给出正确答案和分析 谢谢！
设A(k)∈Cm×n，B(k)∈Cn×l，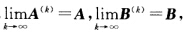
，证明
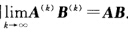
请帮忙给出正确答案和分析，谢谢！
参考解答
490***101
2024-11-11 22:54:41
正确答案：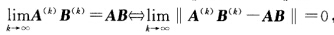
利用矩阵范数的性质有∥A(k) B(k)－AB∥= ∥A(k) B(k)－AB(k)+ AB(k)－AB∥≤∥(A(k)－A)B(k)∥+∥A(B(k)－B∥≤∥B(k)∥∥(A(k)－A)∥+∥A∥∥(B(k)－B)∥由已知条件
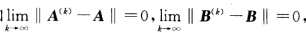及第2题结论知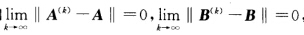
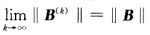．由此可见上面不等式的右边趋于0所以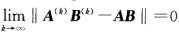
,利用矩阵范数的性质有∥A(k)B(k)－AB∥=∥A(k)B(k)－AB(k)+AB(k)－AB∥≤∥(A(k)－A)B(k)∥+∥A(B(k)－B∥≤∥B(k)∥∥(A(k)－A)∥+∥A∥∥(B(k)－B)∥由已知条件及第2题结论知,．由此可见,上面不等式的右边趋于0,所以
相似问题
验证下列方程组是不相容的 并用A+求它的最佳逼近解． 请帮忙给出正确答案和分析 谢谢！
验证下列方程组是不相容的，并用A+求它的最佳逼近解． 请帮忙给出正确答案和分析，谢谢！
任何n阶矩阵A的高次幂Asup>s(s≥n)必可表示为A的最高不超过n一1次的多项式 当A是可逆矩阵
任何n阶矩阵A的高次幂Asup>s(s≥n)必可表示为A的最高不超过n一1次的多项式，当A是可逆矩阵时，A－1亦然．请帮忙给出正确答案和分析，谢谢！
设A=(αij)n×n λi(i=1 2 … n)为A的特征值 若 证明A是正规矩阵．请帮忙给出正确
设A=(αij)n×n，λi(i=1，2，…，n)为A的特征值，若，证明A是正规矩阵．请帮忙给出正确答案和分析，谢谢！
设A∈Rm×n X∈Rn F(x)=Ax 求请帮忙给出正确答案和分析 谢谢！
设A∈Rm×n，X∈Rn，F(x)=Ax，求请帮忙给出正确答案和分析，谢谢！
设A是n阶可逆实矩阵 则A可表示成一个正交矩阵Q与正定矩阵S的乘积 即A=QS．请帮忙给出正确答案和
设A是n阶可逆实矩阵，则A可表示成一个正交矩阵Q与正定矩阵S的乘积，即A=QS．请帮忙给出正确答案和分析，谢谢！
