任何n阶矩阵A的高次幂Asup>s(s≥n)必可表示为A的最高不超过n一1次的多项式 当A是可逆矩阵

正确答案：不妨设A的特征多项式为△_A(λ)=∣λE一A ∣=λⁿ一α₁λ^n－1+…+(一1)^n－1α_n－1λ+(一1)ⁿα_n．根据凯莱一哈密顿定理可得 △_A(A)=Aⁿ－α₁Aα^n－1+…+(一1)^n－1α_n－1A+(一1)ⁿα_nE=0．当S≥n时用△_A(λ)除λ^s可得λ^s=q(λ).△_A(λ)+r(λ)其中r(λ)的次数小于等于n一1从而A^s=q(A).△_A(A)+r(A)=r(A)． 当A可逆时α_n=∣A∣≠0此时从△_A(A)=0可得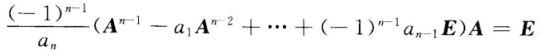由此得到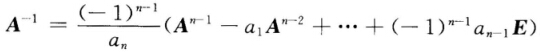
不妨设A的特征多项式为△A(λ)=∣λE一A∣=λn一α1λn－1+…+(一1)n－1αn－1λ+(一1)nαn．根据凯莱一哈密顿定理可得△A(A)=An－α1Aαn－1+…+(一1)n－1αn－1A+(一1)nαnE=0．当S≥n时,用△A(λ)除λs可得λs=q(λ).△A(λ)+r(λ),其中r(λ)的次数小于等于n一1,从而As=q(A).△A(A)+r(A)=r(A)．当A可逆时,αn=∣A∣≠0,此时从△A(A)=0可得由此得到