设曲面M的第3基本形式为Ⅲ=edu2+2fdudv+gdv2. 证明: (1)曲面M的一个双曲点P处
设曲面M的第3基本形式为Ⅲ=edu2+2fdudv+gdv2. 证明: (1)曲面M的一个双曲点P处,在曲率不为零的渐
曲面M的一个双曲点P处,在曲率不为零的渐近曲线上,有
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:由定理2.6.2知Ⅲ一2H.Ⅱ+KG.I=0.沿渐近线有Ⅱ=0故Ⅲ+KGI=0.于是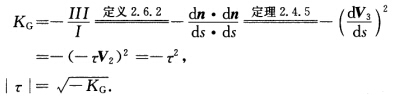
由定理2.6.2,知Ⅲ一2H.Ⅱ+KG.I=0.沿渐近线有Ⅱ=0,故Ⅲ+KGI=0.于是
相似问题
证明:在球面上 任何曲线的测地曲率可写成 其中θ表示曲线与经线的交角 s为曲线x(u(s) v(s)
证明:在球面上,任何曲线的测地曲率可写成 其中θ表示曲线与经线的交角,s为曲线x(u(s),v(s))的弧长参数.再求球面上纬圆的测地曲率(见习题2.8.4图)
设圆柱螺线 设平面上C1曲线z(t)在同一平面内直线l的同一侧 且与l只交于该曲线的正则点P.证明:
设圆柱螺线 设平面上C1曲线z(t)在同一平面内直线l的同一侧,且与l只交于该曲线的正则点P.证明:直设平面上C1曲线z(t)在同一平面内直线l的同一侧,且与l
R3中k≠0 τ≠0的C4连通曲线x(s)为球面曲线等价于设C:x(s)(s0≤s≤s1)为球面挠闭
R3中k≠0,τ≠0的C4连通曲线x(s)为球面曲线等价于设C:x(s)(s0≤s≤s1)为球面挠闭曲线(τ(s)≠0,).证明:设C:x(s)(s0≤s≤s1)为球面挠闭曲线(τ(s)≠0
设P为R3中光滑曲面M上的一点.证明:当P不为脐点时 M的主曲率k1 k2(总假定k1≤k2)为P附
设P为R3中光滑曲面M上的一点.证明:当P不为脐点时,M的主曲率k1,k2(总假定k1≤k2)为P附近的光滑函数;当P为脐点时,主曲率,k1,k2为P附近的连续函数.
此时 Liouville公式可写成请帮忙给出正确答案和分析 谢谢!
此时,Liouville公式可写成请帮忙给出正确答案和分析,谢谢!












