设V1 V2是线性空间V的两个非平凡子空间 证明:在V中存在α 使αV1 αV2同时成立.请帮忙给出
设V1,V2是线性空间V的两个非平凡子空间,证明:在V中存在α,使α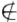 V1,α
V1,α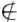 V2同时成立.
V2同时成立.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:法1 因为V1V2都是非平凡子空间故存在向量αβ使α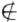 V1β
V1β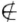 V2如果有α
V2如果有α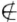 V2则α即为所求向量.假设α∈V2则对数域F中任意数k有kα+β
V2则α即为所求向量.假设α∈V2则对数域F中任意数k有kα+β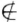 V2若不然则由于α∈V2故kα∈V2于是β=(kα+β)-kα∈V2这与β
V2若不然则由于α∈V2故kα∈V2于是β=(kα+β)-kα∈V2这与β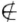 V2矛盾.现取k1≠k2则k1α+β. k2α+β不可能都属于V1若不然则(k1α+β)-(k2α+β)=(k1-k1)α∈1于是α= 1
V2矛盾.现取k1≠k2则k1α+β. k2α+β不可能都属于V1若不然则(k1α+β)-(k2α+β)=(k1-k1)α∈1于是α= 1 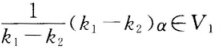 这与
这与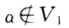 。矛盾故k1α+βk2α+β中至少有一个不属于V1同时它也不属于V2即为所求向量. 法2 因为V1是非平凡子空间故存在
。矛盾故k1α+βk2α+β中至少有一个不属于V1同时它也不属于V2即为所求向量. 法2 因为V1是非平凡子空间故存在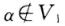 如果
如果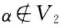 则结论成立.若α∈V2则由于V2也是非平凡子空间故存在向量
则结论成立.若α∈V2则由于V2也是非平凡子空间故存在向量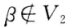 若
若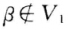 则结论成立若β∈V1则有
则结论成立若β∈V1则有 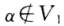 β∈V1;α∈V2
β∈V1;α∈V2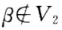 .于是可推得
.于是可推得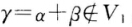 并且
并且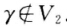 .
.
法1因为V1,V2都是非平凡子空间,故存在向量α,β,使αV1,βV2如果有αV2,则α即为所求向量.假设α∈V2,则对数域F中任意数k,有kα+βV2,若不然,则由于α∈V2,故kα∈V2,于是β=(kα+β)-kα∈V2,这与βV2矛盾.现取k1≠k2,则k1α+β.k2α+β不可能都属于V1,若不然,则(k1α+β)-(k2α+β)=(k1-k1)α∈1,于是α=1,这与。矛盾,故k1α+β,k2α+β中至少有一个不属于V1,同时它也不属于V2,即为所求向量.法2因为V1,是非平凡子空间,故存在,如果,则结论成立.若α∈V2,则由于V2也是非平凡子空间,故存在向量,若,则结论成立,若β∈V1,则有,β∈V1;α∈V2,.于是可推得,并且.
相似问题
设X1 X2 … Xn是来自正态总体N(μ σ2)的一个简单随机样本 S2为其样本方差 且若样本容量
设X1,X2,…,Xn是来自正态总体N(μ,σ2)的一个简单随机样本,S2为其样本方差,且若样本容量n满足χ0 052(0一1)≥38.9,求满足上述条件的n的最小值.
设总体X~N(μ σ2) X1 X2 … Xn为来自总体X的样本 当用用传统工艺加工的某种水果罐头中
设总体X~N(μ,σ2),X1,X2,…,Xn为来自总体X的样本,当用用传统工艺加工的某种水果罐头中,每瓶平均维用传统工艺加工的某种水果罐头中,每瓶平均维
设f(x1 x2 … xn)=XTAX是一实二次型 λ1 λ2 … λn是A的特征值 且λ1≤λ2≤
设f(x1,x2,…,xn)=XTAX是一实二次型,λ1,λ2,…,λn是A的特征值,且λ1≤λ2≤…≤λn证明:对设二次型f(x1,x2,设二次型f(x1,x2,…,xn对应的
设T是线性空间V上的线性变换 如果Tk-1(ξ)≠0 但Tk(ξ)=0.求证ξ T(ξ) … Tk
设T是线性空间V上的线性变换,如果Tk-1(ξ)≠0,但Tk(ξ)=0.求证ξ,T(ξ),…, Tk-1(ξ)(k>0)线性无关.请帮忙给出正确答案和分析,谢谢!
设A是n阶实对称矩阵 且A2=E.证明:存在正交矩阵Q 使得请帮忙给出正确答案和分析 谢谢!
设A是n阶实对称矩阵,且A2=E.证明:存在正交矩阵Q,使得请帮忙给出正确答案和分析,谢谢!












