设A为三阶方阵 有3个不同的特征值λ1 λ2 λ3对应的特征向量依次为α1 α2 α3 令β=α1+

正确答案：Aα₁=λ_iα_i(i=123) 因此Aβ=A(α₁+α₂+α₃)=Aα₁+Aα₂+Aα₃=λ₁a₁+λ₂a₂+λ₃a₃ A²β=A(Aβ)=A(λ₁α₁+λ₂α₂+λ₃α₃)=λ₁²α₁+λ₂²α₂+λ₃²α₃ 设存在3个常数k₁k₂k₃使k₁β+k₂Aβ+k₃A²β=0． 即 k₁(α₁+α₂+α₃)+k₂(λα₁+λα₂+λα₃)+k₃(λ₁²α+λ₂²α+λ₃²α)=(k₁+k₂λ₁+k₃λ₁²)α₁+(k₁+k₂λ₂+k₃λ₂²)α₂+(k₁+k₂λ₃+k₃λ₃²)α₃=0由于不同特征值的特征向量线性无关所以α₁α₂α₃线性无关于是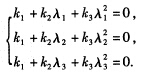其系数行列式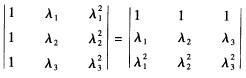=(λ₂一λ₁)(λ₃一λ₁)(λ₃)一λ₂≠0因此方程组仅有零解k₁=k₂=k₃=0故βAβA²β线性无关．
Aα1=λiαi(i=1,2,3)因此Aβ=A(α1+α2+α3)=Aα1+Aα2+Aα3=λ1a1+λ2a2+λ3a3,A2β=A(Aβ)=A(λ1α1+λ2α2+λ3α3)=λ12α1+λ22α2+λ32α3设存在3个常数k1,k2,k3,使k1β+k2Aβ+k3A2β=0．即k1(α1+α2+α3)+k2(λα1+λα2+λα3)+k3(λ12α+λ22α+λ32α)=(k1+k2λ1+k3λ12)α1+(k1+k2λ2+k3λ22)α2+(k1+k2λ3+k3λ32)α3=0,由于不同特征值的特征向量线性无关,所以α1,α2,α3线性无关,于是其系数行列式=(λ2一λ1)(λ3一λ1)(λ3)一λ2≠0,因此方程组仅有零解k1=k2=k3=0,故β,Aβ,A2β线性无关．