设n阶矩阵A B满足R(A)+R(B)＜n 证明A与B有公共的特征值 有公共的特征向量．请帮忙给出正
设n阶矩阵A、B满足R(A)+R(B)＜n，证明A与B有公共的特征值、有公共的特征向量．
请帮忙给出正确答案和分析，谢谢！
参考解答
413***101
2024-11-11 04:05:18
正确答案：显然R(A)＜n．另一方面R(A)＜nA不可逆0是A的特征值；同理0也是B的特征值于是A与B有公共的特征值0．A与B有对应于λ=0的特征向量依次是方程Ax=0和Bx=0的非零解．于是A与B有对应于λ=0的公共特征向量
另一方面由矩阵秩的性质⑤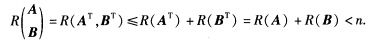
综上A与B有公共的特征向量．
显然R(A)＜n．另一方面,R(A)＜n,A不可逆,0是A的特征值；同理,0也是B的特征值,于是A与B有公共的特征值0．A与B有对应于λ=0的特征向量依次是方程Ax=0和Bx=0的非零解．于是,A与B有对应于λ=0的公共特征向量另一方面,由矩阵秩的性质⑤综上,A与B有公共的特征向量．
相似问题
已知α=(1 一2 2)T是二次型xTAx=ax12+4x22+bx32一4x1x2+4x1x3—8
已知α=(1，一2，2)T是二次型xTAx=ax12+4x22+bx32一4x1x2+4x1x3—8x2x3矩阵A的特征向量，求正交换化二次型为标准形，并写出所用正交变换．请帮忙给出正确答案和分析，谢谢！
试求一个正交的相似变换矩阵 将下列对称阵化为对角阵： 请帮忙给出正确答案和分析 谢谢！
试求一个正交的相似变换矩阵，将下列对称阵化为对角阵： 请帮忙给出正确答案和分析，谢谢！
若面对圆偏振光传播方向向光源看过去 光矢量顶端的轨迹顺时针旋转称为_______ 逆时针旋转称为__
若面对圆偏振光传播方向向光源看过去，光矢量顶端的轨迹顺时针旋转称为_______，逆时针旋转称为_______。请帮忙给出正确答案和分析，谢谢！
已知三阶矩阵A的特征值为1 2 一3 求|A*+3A+2E|．请帮忙给出正确答案和分析 谢谢！
已知三阶矩阵A的特征值为1，2，一3，求|A*+3A+2E|．请帮忙给出正确答案和分析，谢谢！
已知向量组 证明B组能由A组线性表示 但A组不能由B组线性表示．请帮忙给出正确答案和分析 谢谢！
已知向量组 证明B组能由A组线性表示，但A组不能由B组线性表示．请帮忙给出正确答案和分析，谢谢！
