已知三阶矩阵A与三维列向量x满足A3x=3Ax—A2x 且向量组x Ax A2x线性无关． (1)记

正确答案：(1)因方阵P的列向量组线性无关故P可逆从而B=P^-1AP． 记向量y=Axz=A²x则所给矩阵P可写为P=(xyz)并且由分块矩阵乘法法则有AP=A(xyz)=(AxAyAz)因Ax=yAy=zAz=A³x3Ax—A²x=3y-z故 AP=(yz3y—z)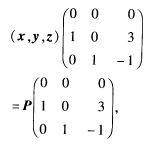于是 B=P^-1AP=(其实矩阵B就是向量组AxAyAz由向量组xyz线性表示的系数矩阵．)(2)由B=P^-1AP两边取行列式便有|A|=|B|=0．
(1)因方阵P的列向量组线性无关,故P可逆,从而B=P-1AP．记向量y=Ax,z=A2x,则所给矩阵P可写为P=(x,y,z),并且由分块矩阵乘法法则,有AP=A(x,y,z)=(Ax,Ay,Az),因Ax=y,Ay=z,Az=A3x3Ax—A2x=3y-z,故AP=(y,z,3y—z)于是B=P-1AP=(其实,矩阵B就是向量组Ax,Ay,Az由向量组x,y,z线性表示的系数矩阵．)(2)由B=P-1AP,两边取行列式,便有|A|=|B|=0．