设f(x1 x2 … xn)=XTAX是一实二次型 λ1 λ2 … λn是A的特征值 且λ1≤λ2≤

正确答案：设A是n维欧氏空间V上的任一正交变换取V的一组标准正交基ε₁ε₂…ε_n则η₁=A(ε₁)η₂=A(ε₂)…η_n一A(ε_n)也是V的一组标准正交基此时若η₁=ε₁η₂=ε₂…η_n=ε_n则A是一个恒等变换只要作镜面反射A₁(γ)=)γ－2(ε₁γ)ε₁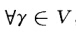．则有A₁(ε₁)=－ε₁A₁(ε_j)=ε_j(j=23…n)且A=A₁A₁结论成立． 若ε₁ε₂…ε_n与η₁η₂…η_n不全相同不妨设η₁≠ε₁则η₁ε₁为两个不同的单位向量由上面第20题知存在镜面反射A₁使A₁(ε₁)=η₁．令A₁(ε_j)=ξ(j=23…n)若ξ_j=η_j(j=23…n)则A=A₁结论成立．否则可设ξ₂≠η₂再作镜面反射A₂(γ)=γ－2(ηγ)η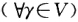其中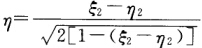则A₂(ξ)=η₂因为(η₁η₂)=0(ξ₂₁)=0所以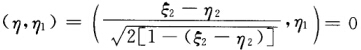且A₂(η₁)=η－2(ηη₁)η=η₁A₂(ξ_i)=ξ_i(i=3…n)．如此继续下去设=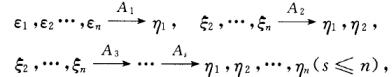则A=A_sA_s－1…A₂A₁其中A_i(j=12…s)都是镜面反射证毕．
设A是n维欧氏空间V上的任一正交变换,取V的一组标准正交基ε1,ε2,…,εn,则η1=A(ε1),η2=A(ε2),…,ηn一A(εn)也是V的一组标准正交基,此时,若η1=ε1,η2=ε2,…,ηn=εn,则A是一个恒等变换,只要作镜面反射A1(γ)=)γ－2(ε1,γ)ε1,．则有A1(ε1)=－ε1,A1(εj)=εj,(j=2,3,…,n),且A=A1A1,结论成立．若ε1,ε2,…,εn与η1,η2,…,ηn不全相同,不妨设η1≠ε1,则η1,ε1为两个不同的单位向量,由上面第20题知,存在镜面反射A1,使A1(ε1)=η1．令A1(εj)=ξ(j=2,3,…,n),若ξj=ηj(j=2,3,…,n),则A=A1,结论成立．否则可设ξ2≠η2,再作镜面反射A2(γ)=γ－2(η,γ)η,其中,则A2(ξ)=η2,因为(η1,η2)=0,(ξ2,1)=0,所以且A2(η1)=η－2(η,η1)η=η1,A2(ξi)=ξi(i=3,…,n)．如此继续下去,设=则A=AsAs－1…A2A1,其中Ai(j=1,2,…,s)都是镜面反射,证毕．