设 f(x1 x2 … xn)是一个秩为n的二次型 证明:有Rn的一个维子空间V1存在(s为符号差数
设 f(x1,x2,…,xn)是一个秩为n的二次型,证明:有Rn的一个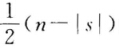 维子空间V1存在(s为符号差数),使对任意的(x1,x2,…,xn)∈V1,都有f(x1,x2,…,xn)=0.
维子空间V1存在(s为符号差数),使对任意的(x1,x2,…,xn)∈V1,都有f(x1,x2,…,xn)=0.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:设f的正惯性指数为p负惯性指数为qp+q=n.则存在可逆矩阵CY=CX使得f=y12+…+yp2-yp-12-…-yp+q2因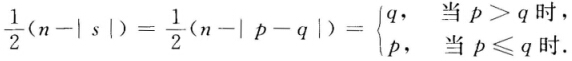 故下面仅就p≤q时给出证明(当p>q时同理可证). 将Y=CX展开可得方程组
故下面仅就p≤q时给出证明(当p>q时同理可证). 将Y=CX展开可得方程组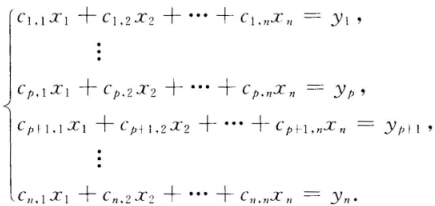 取向量 ε1=(10…010…0)ε2=(01…001…0)… εp=(00…100…1…0).显然ε1ε2…εp线性无关代人Y=CX方程组中可得解α1α2…αp线性无关且满足Cα1=ε1Cα2=ε2…Cαp=εp.下面证P维子空间L(α1α2…αp)即为所求空间V1. 设x0∈V1且满足关系x0=k1α1+k2α2+…+kpαp则y0=Cx0=k1Cα1+k2Cα2+…+kpCαp=k1ε1+k2ε2+…+kpεp代人二次型.f中可得
取向量 ε1=(10…010…0)ε2=(01…001…0)… εp=(00…100…1…0).显然ε1ε2…εp线性无关代人Y=CX方程组中可得解α1α2…αp线性无关且满足Cα1=ε1Cα2=ε2…Cαp=εp.下面证P维子空间L(α1α2…αp)即为所求空间V1. 设x0∈V1且满足关系x0=k1α1+k2α2+…+kpαp则y0=Cx0=k1Cα1+k2Cα2+…+kpCαp=k1ε1+k2ε2+…+kpεp代人二次型.f中可得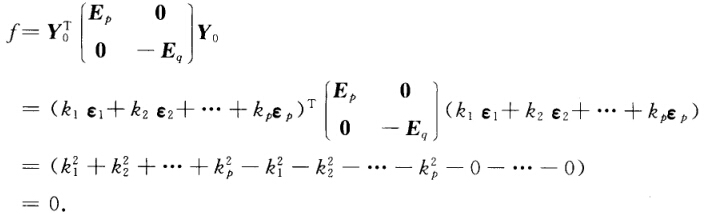
设f的正惯性指数为p,负惯性指数为q,p+q=n.则存在可逆矩阵C,Y,=CX,使得f=y12+…+yp2-yp-12-…-yp+q2,因故下面仅就p≤q时给出证明(当p>q时同理可证).将Y=CX展开可得方程组取向量ε1=(1,0,…,0,1,0,…,0),ε2=(0,1,…,0,0,1,…,0),…εp=(0,0,…1,0,0,…,1,…,0).显然ε1,ε2,…,εp线性无关,代人Y=CX方程组中可得解α1,α2,…,αp线性无关,且满足Cα1=ε1,Cα2=ε2,…,Cαp=εp.下面证P维子空间L(α1,α2,…,αp)即为所求空间V1.设x0∈V1,且满足关系x0=k1α1+k2α2+…+kpαp,则y0=Cx0=k1Cα1+k2Cα2+…+kpCαp=k1ε1+k2ε2+…+kpεp,代人二次型.f中可得
相似问题
设一个汽车站上 某路公共汽车每5分钟有一辆车到达 页乘客在5分钟内任一时间到达是等可能的 试计算在车
设一个汽车站上,某路公共汽车每5分钟有一辆车到达,页乘客在5分钟内任一时间到达是等可能的,试计算在车站候车的10位乘客中只有1位等待时间超过4分钟的
设随机变量X的分布函数为设随机变量X服从N(μ σ2) 试求P{|X一μ|<σ}的值.已知标准正态分
设随机变量X的分布函数为设随机变量X服从N(μ,σ2),试求P{|X一μ|<σ}的值.已知标准正态分布函数φ(x)设随机变量X服从N(μ,σ2),试求P{|X一μ|
如果T1 T2 … Ts是线性空间V的s个两两不同的线性变换 则V中必存在向量α 使T1α T2α
如果T1,T2,…,Ts是线性空间V的s个两两不同的线性变换,则V中必存在向量α,使T1α,T2α,…,Tsα也两两不同.请帮忙给出正确答案和分析,谢谢!
设ξ η是相互独立的 且概率密度分别为试述随机变量的分类.试述随机变量的分类.请帮忙给出正确答案和分
设ξ,η是相互独立的,且概率密度分别为试述随机变量的分类.试述随机变量的分类.请帮忙给出正确答案和分析,谢谢!
设总体X服从正态分布N(10 32) X1 X2 … X6是它的一组样本 容量为9的随机样本平均寿命
设总体X服从正态分布N(10,32),X1,X2,…,X6是它的一组样本,容量为9的随机样本平均寿命落在4.4~5.2年之间的概率;请帮忙给出正确答案和分析,谢谢!












