设四元线性方程组(Ⅰ)为又已知齐次线性方程组(Ⅱ)的通解为k1(0 1 1 0)T+k2(一1 2
设四元线性方程组(Ⅰ)为
又已知齐次线性方程组(Ⅱ)的通解为k1(0，1，1，0)T+k2(一1，2，2，1)T． (1)求方程组(Ⅰ)的基础解系． (2)问线性方程组(Ⅰ)和(Ⅱ)是否有非零公共解?若有，则求出所有的非零公共解；若没有，则说明理由．
请帮忙给出正确答案和分析，谢谢！
参考解答
456***101
2024-11-11 14:08:05
正确答案：(1)方程组(Ⅰ)的系数矩阵为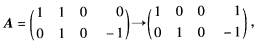
故(Ⅰ)的基础解系为η1=(0010)η2=(一1101)．(2) 将(Ⅱ)的通解代入方程组(Ⅰ)则有
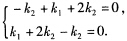解得k1=一k2则向量 k1(0110)+k2(一1221)=一k2(0110)+k2(一1221)=k2(一1111) 是方程组(Ⅰ)、(Ⅱ)的公共解． 当k2≠0时有k2(一1111)≠0 故方程组(Ⅰ)、(Ⅱ)的所有非零公共解是k(一1111)其中k是任意非零常数．
(1)方程组(Ⅰ)的系数矩阵为故(Ⅰ)的基础解系为η1=(0,0,1,0),η2=(一1,1,0,1)．(2)将(Ⅱ)的通解代入方程组(Ⅰ),则有解得k1=一k2,则向量k1(0,1,1,0)+k2(一1,2,2,1)=一k2(0,1,1,0)+k2(一1,2,2,1)=k2(一1,1,1,1)是方程组(Ⅰ)、(Ⅱ)的公共解．当k2≠0时,有k2(一1,1,1,1)≠0,故方程组(Ⅰ)、(Ⅱ)的所有非零公共解是k(一1,1,1,1),其中k是任意非零常数．
相似问题
某海事法院根据当事人甲进出口公司的请求 对承运其进口货物的乙海运公司所属的某船舶的航海日志予以复制。
某海事法院根据当事人甲进出口公司的请求，对承运其进口货物的乙海运公司所属的某船舶的航海日志予以复制。这一强制措施属于( )A、简易程序B、督促程序C
已知线性方程组 (1)a b为何值时 方程组有解? (2)方程组有解时 求出其导出组的一个基础解系
已知线性方程组 (1)a，b为何值时，方程组有解? (2)方程组有解时，求出其导出组的一个基础解系． (3)方程组有解时，求出方程组的全部解．请帮忙给出
λ取何值时 非齐次线性方程组 (1)有唯一解；(2)无解；(3)有无穷多解?请帮忙给出正确答案和分析
λ取何值时，非齐次线性方程组 (1)有唯一解；(2)无解；(3)有无穷多解?请帮忙给出正确答案和分析，谢谢！
如图1-29所示 在光滑水平地面上 质量分别为m1 m2木块 位于x轴上 开始时静止。用一根质量可忽
如图1-29所示，在光滑水平地面上，质量分别为m1，m2木块，位于x轴上，开始时静止。用一根质量可忽略，弹性系数为k，原长为l0的轻弹簧相连。用外力F=一Fi
如图1—16(a)所示 在竖直平面xOy内 使一个质点从给定点P(x0 y0)沿光滑直线轨道由静止运
如图1—16(a)所示，在竖直平面xOy内，使一个质点从给定点P(x0，y0)沿光滑直线轨道由静止运动到一个给定的圆x2+y2=1上，求质点采取什么路径用时最少。 请
