如图1—16(a)所示 在竖直平面xOy内 使一个质点从给定点P(x0 y0)沿光滑直线轨道由静止运
如图1—16(a)所示，在竖直平面xOy内，使一个质点从给定点P(x0，y0)沿光滑直线轨道由静止运动到一个给定的圆x2+y2=1上，求质点采取什么路径用时最少。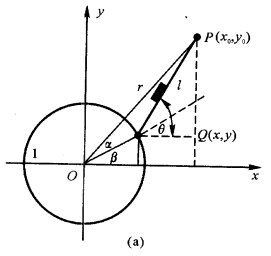 
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***101
2024-11-11 13:49:34
正确答案：设由P点到Q点的直线路径用时最少各个参数如图1-16(a)所示斜面长为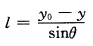
l2=1+r2一2rcosα从P到Q用时为tOP与x轴的夹角为α0且y0=rsinα0故
y1=sinβ=sin(α0一α)=sinα0cosα—cosα0sinα=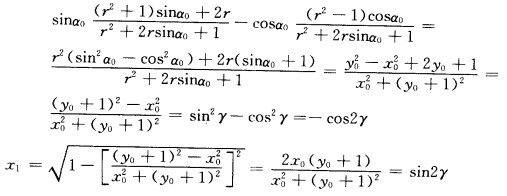
可证
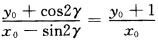由此知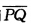
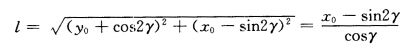
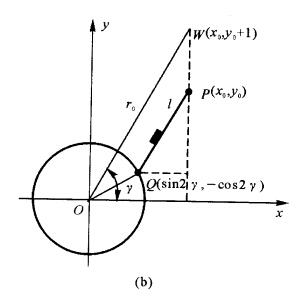平行OW．则有作图法如下：由P向x轴作垂线反向延长l得W点连接O与W过P作直线平行OW与圆环的近侧交于Q(sin2γ一cos2γ)点PQ即为所求用时最少的直线路径如图1—16(b)所示。此时路径长为
最小用时为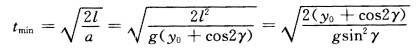
设由P点到Q点的直线路径用时最少,各个参数如图1-16(a)所示,斜面长为l2=1+r2一2rcosα从P到Q用时为t,OP与x轴的夹角为α0,且y0=rsinα0,故y1=sinβ=sin(α0一α)=sinα0cosα—cosα0sinα=可证由此知平行OW．则有作图法如下：由P向x轴作垂线反向延长l得W点,连接O与W过P作直线平行OW与圆环的近侧交于Q(sin2γ一cos2γ)点,PQ即为所求用时最少的直线路径,如图1—16(b)所示。此时路径长为最小用时为
相似问题
设A∈Cn×n x∈Rn×n A≥0 x≥0 β≥0 若Ax＜βx(Ax≤βx) 证明γ(A)
设A∈Cn×n，x∈Rn×n，A≥0，x≥0，β≥0，若Ax＜βx(Ax≤βx)，证明γ(A)<β(γ(A)≤β)不一定成立．请帮忙给出正确答案和分析，谢谢！
设AP=PA 其中 求φ(A)=A8(5E一6A+A2)．请帮忙给出正确答案和分析 谢谢！
设AP=PA，其中 求φ(A)=A8(5E一6A+A2)．请帮忙给出正确答案和分析，谢谢！
质量为m的小球系在不可伸长的细线的一端 细线的另一端系于一根竖直的固定圆柱的轴线的上端 给小球以初速
质量为m的小球系在不可伸长的细线的一端，细线的另一端系于一根竖直的固定圆柱的轴线的上端，给小球以初速，使细线缠绕(无滑动地)在圆柱上，如图1—10所
一根长l的匀质链条 一部分放在光滑桌面上 另一部分从桌边下垂 长为a 由静止释放 如图1—21所示。
一根长l的匀质链条，一部分放在光滑桌面上，另一部分从桌边下垂，长为a，由静止释放，如图1—21所示。求链条的运动方程。 请帮忙给出正确答案和分析，谢谢！
设非齐次线性方程组Ax=b的系数矩阵的秩为r 向量η1 ηn-r+1是它的n一r+1个线性无关的解．
设非齐次线性方程组Ax=b的系数矩阵的秩为r，向量η1，ηn-r+1是它的n一r+1个线性无关的解．试证它的任一解可表示为 x=k1η1+…+kn-r+1ηn-r+1(其中，k1+
