设曲面M1与M2沿着曲线C相切(即有相同的单位法向聆) C为曲面M1的测地线.证明:C也为M2的测地
设曲面M1与M2沿着曲线C相切(即有相同的单位法向聆),C为曲面M1的测地线.证明:C也为M2的测地线.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:如果k(s0)>0则由连续性存在开邻域(s0一δx0+δ)使k(s)>0.因M1与M2沿C相切即M1与M2沿C有相同的单位法向量.而C为M1的测地线根据定理2.8.4(4)n=±V2.再一次应用定理2.8.4(4)C在(s0一δs0+δ)这一段也为测地线.如果存在(ab)使k(s)=0(a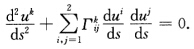 根据
根据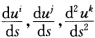 的连续性知整个C上关于M2满足上述测地线方程所以C为M2上的测地线.
的连续性知整个C上关于M2满足上述测地线方程所以C为M2上的测地线.
如果k(s0)>0,则由连续性,存在开邻域(s0一δ,x0+δ)使k(s)>0.因M1与M2沿C相切,即M1与M2沿C有相同的单位法向量.而C为M1的测地线,根据定理2.8.4(4),n=±V2.再一次应用定理2.8.4(4),C在(s0一δ,s0+δ)这一段也为测地线.如果存在(a,b)使k(s)=0(a1,M2上的测地线段.综上知,C在上述两类点上关于M2为测地线,它满足测地线方程:根据的连续性知,整个C上关于M2满足上述测地线方程,所以C为M2上的测地线.
相似问题
求曲线x(t)=(a(3t—t3) 3at2 a(3t+t3)) (a>0)的曲率 挠率.请帮忙给出
求曲线x(t)=(a(3t—t3),3at2,a(3t+t3)) (a>0)的曲率、挠率.请帮忙给出正确答案和分析,谢谢!
设曲线的参数变换为(θ为常数).求第1基本形式系数的变换式.请帮忙给出正确答案和分析 谢谢!
设曲线的参数变换为(θ为常数).求第1基本形式系数的变换式.请帮忙给出正确答案和分析,谢谢!
(Dupin定理)在R3中 证明:三族互相正交的曲面交线必为所在曲面的曲率线.请帮忙给出正确答案和分
(Dupin定理)在R3中,证明:三族互相正交的曲面交线必为所在曲面的曲率线.请帮忙给出正确答案和分析,谢谢!
曲线C1:u+v=0和C2:u一v=0的交角θ;1. 求下列曲面M的第1基本形式和第2基本形式I Ⅱ
曲线C1:u+v=0和C2:u一v=0的交角θ;1 求下列曲面M的第1基本形式和第2基本形式I,Ⅱ: (1)椭球面:参数表示为X(Φ,Θ)=(ACOSΦCOSΘ,BCOS ΦSINΘ
设s为弧长 在R3中证明:(x x x)=k2τ(x x x)=k2τ请帮忙给出正确答案和分析 谢谢
设s为弧长,在R3中证明:(x,x,x)=k2τ(x,x,x)=k2τ请帮忙给出正确答案和分析,谢谢!












