曲线C1：u+v=0和C2：u一v=0的交角θ；1. 求下列曲面M的第1基本形式和第2基本形式I Ⅱ
曲线C1：u+v=0和C2：u一v=0的交角θ；
1. 求下列曲面M的第1基本形式和第2基本形式I，Ⅱ： (1)椭球面：
参数表示为X(Φ，Θ)=(ACOSΦCOSΘ，BCOS ΦSINΘ，CSINΦ)； (2)单叶双曲面
参数表示为X(U，V)=(ACH UCOSV，BCH USINV，CSHU)； (3)双叶双曲面
参数表示为X(U，V)=(ACHU，BSH UCOSV，CSH USINV)； (4)椭圆抛物面：
参数表示为
(5)双曲抛物线
参数表示为X(U，V)=(A(U+V)，B(U一V)，2UV)； (6)劈锥曲面：X(U，V)=(UCOSV，USINV，Φ(V))，Φ为C1函数； (7)
参数表示为X(U，V)=(A(U+V)，B(U—V)，U2+V2).
请帮忙给出正确答案和分析，谢谢！
参考解答
406***102
2024-11-17 02:04:38
正确答案：I=Edu2+2Fdudv+Gdv2=du2+(v2+a2)dv2C1：u+v=0du+dv=0C2：u一v=0δu一δv=0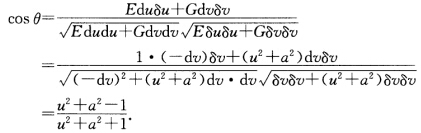
于是两线C1：u+v=0与C2：u一v=0的交点(00)处的交角θ的余弦为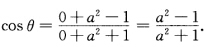
I=Edu2+2Fdudv+Gdv2=du2+(v2+a2)dv2,C1：u+v=0,du+dv=0,C2：u一v=0,δu一δv=0,于是,两线C1：u+v=0与C2：u一v=0的交点(0,0)处的交角θ的余弦为
相似问题
设s为弧长 在R3中证明：(x x x)=k2τ(x x x)=k2τ请帮忙给出正确答案和分析 谢谢
设s为弧长，在R3中证明：(x，x，x)=k2τ(x，x，x)=k2τ请帮忙给出正确答案和分析，谢谢！
证明：柱面M上 k≠0的测地线C为一般螺线．请帮忙给出正确答案和分析 谢谢！
证明：柱面M上，k≠0的测地线C为一般螺线．请帮忙给出正确答案和分析，谢谢！
设x(t)为空间R3中的曲线 曲率为k(t) 挠率为τ(t) 求曲线的曲率请帮忙给出正确答案和分析
设x(t)为空间R3中的曲线，曲率为k(t)，挠率为τ(t)，求曲线的曲率请帮忙给出正确答案和分析，谢谢！
设曲面M的第1基本形式为求KG．求KG．请帮忙给出正确答案和分析 谢谢！
设曲面M的第1基本形式为求KG．求KG．请帮忙给出正确答案和分析，谢谢！
证明：对于曲面M上的一点 若KG>0 则不存在实的渐近方向；若KG
证明：对于曲面M上的一点，若KG>0，则不存在实的渐近方向；若KG<0，则存在两个渐近方向，且主方向平分两渐近方向所张成的角．请帮忙给出正确答案和分析，
