证明：对于曲面M上的一点 若KG>0 则不存在实的渐近方向；若KG

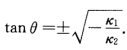正确答案：证法1 (1)根据定义2．4．3渐近方向满足微分方程：Ldu²+2Mdudv+Ndv²=0．它是2次方程有实解的条件为△=(2M)²一4LN=4(M²一LN)≥0即K_G=当K_G<0时有两个相异的实渐近方向；当K_G=0时有两个相同的渐近方向；当K_G>0时无实的渐近方向．(2)设K_G<0．根据定义2．5．1与定理2．5．3中的Euler公式对于在渐近方向的法曲率有0=k_n=k₁cos²θ+k₂sin²θ其中θ为渐近方向与主方向的夹角．于是这表明两个渐近方向与主方向的夹角相等．证法2 (2)当K_G<0时取两族渐近曲线为参数网则dv=0Ldu²=0L=0du=0 Ndv²=0 N=0．于是曲率线微分方程(参阅定理2．5．5)为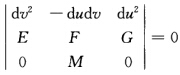即M(Edu²一Gdv²)=0．因为L=N=0K_G<0所以M≠0．从而上式即为Edu²一Gdv²=0．设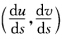在曲面M上平分两渐近方向(10)与(01)所张成的角即这正说明了两渐近方向的角平分线就是曲面M上的曲率线．
证法1(1)根据定义2．4．3,渐近方向满足微分方程：Ldu2+2Mdudv+Ndv2=0．它是2次方程,有实解的条件为△=(2M)2一4LN=4(M2一LN)≥0,即KG=当KG<0时,有两个相异的实渐近方向；当KG=0时,有两个相同的渐近方向；当KG>0时,无实的渐近方向．(2)设KG<0．根据定义2．5．1与定理2．5．3中的Euler公式,对于在渐近方向的法曲率,有0=kn=k1cos2θ+k2sin2θ,其中θ为渐近方向与主方向的夹角．于是这表明两个渐近方向与主方向的夹角相等．证法2(2)当KG<0时,取两族渐近曲线为参数网,则dv=0,Ldu2=0,L=0,du=0,Ndv2=0,N=0．于是,曲率线微分方程(参阅定理2．5．5)为即M(Edu2一Gdv2)=0．因为L=N=0,KG<0,所以M≠0．从而上式即为Edu2一Gdv2=0．设在曲面M上平分两渐近方向(1,0)与(0,1)所张成的角,即这正说明了两渐近方向的角平分线就是曲面M上的曲率线．