设P0为两曲线x(s)与设k(s0)≠0.证明:曲线C:x(s)(s为其弧长)与已给球面(球心为m)
设P0为两曲线x(s)与设k(s0)≠0.证明:曲线C:x(s)(s为其弧长)与已给球面(球心为m)在s0有2阶接触其中
设k(s0)≠0.证明:曲线C:x(s)(s为其弧长)与已给球面(球心为m)在s0有2阶接触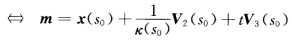 其中t可以任意选定.上式右边当固定s0时得到一条直线,称为曲线x(s)在s0处的曲率轴或极轴,而点
其中t可以任意选定.上式右边当固定s0时得到一条直线,称为曲线x(s)在s0处的曲率轴或极轴,而点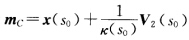 称为曲率中心,以曲率中心为圆心、
称为曲率中心,以曲率中心为圆心、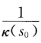 为半径的圆落在密切平面上,称为曲线x(s)在s0处的密切圆(见习题1.4.3图).(2)设k(s0)≠0,τ(s0)
为半径的圆落在密切平面上,称为曲线x(s)在s0处的密切圆(见习题1.4.3图).(2)设k(s0)≠0,τ(s0)
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:证法1(1)设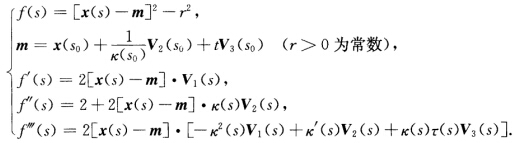 由此知x(s)在x(s0)与球面(x一m)2=r2有2阶接触等价于
由此知x(s)在x(s0)与球面(x一m)2=r2有2阶接触等价于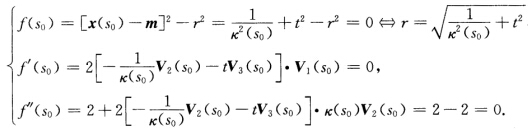 (2)x(s)在x(s0)与球面(x一m)2=r2有3阶接触等价于
(2)x(s)在x(s0)与球面(x一m)2=r2有3阶接触等价于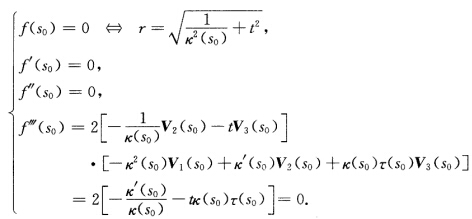 此时
此时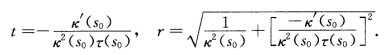 证法2设f(s)=[x(s)一m2一r2m=x(s0)+uV2(s)+tV3(s)则
证法2设f(s)=[x(s)一m2一r2m=x(s0)+uV2(s)+tV3(s)则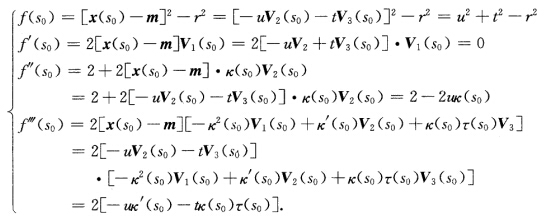 (1)x(s)在s0与球面(x一m)2=r2=u2+t2有2阶接触等价于
(1)x(s)在s0与球面(x一m)2=r2=u2+t2有2阶接触等价于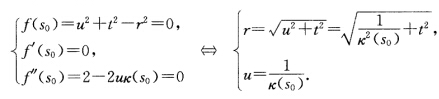 (2)x(s)在s0与球面(x—m)2=r2=u2+t2有3阶接触等价于
(2)x(s)在s0与球面(x—m)2=r2=u2+t2有3阶接触等价于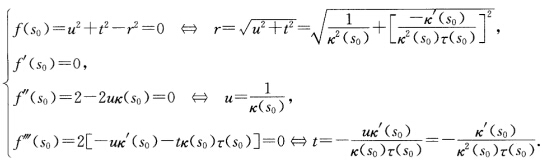 由上立知题中所有结论.证法3 参阅习题1.3.22证法2应用Taylor展开.(1)设球面中心为
由上立知题中所有结论.证法3 参阅习题1.3.22证法2应用Taylor展开.(1)设球面中心为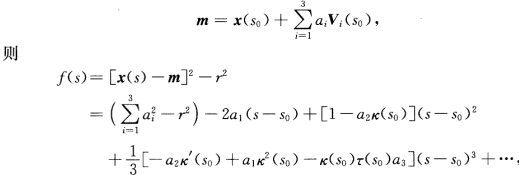 x(s)与球面(x—m)2=r2之间的k阶接触如下:
x(s)与球面(x—m)2=r2之间的k阶接触如下: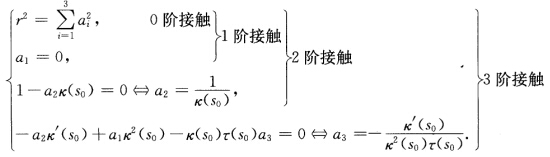 这表明:(a)球心
这表明:(a)球心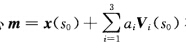 在任何点只要球面经过x(s0)(即半径r=
在任何点只要球面经过x(s0)(即半径r=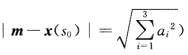 x(s)与球面(x—m)2=r2在x(s0)处就是0阶接触.(b)当
x(s)与球面(x—m)2=r2在x(s0)处就是0阶接触.(b)当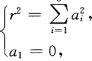 且球心在
且球心在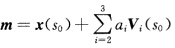 的任何点时x(s)与球面(x—m)2=r2在x(s0)处是1阶接触.
的任何点时x(s)与球面(x—m)2=r2在x(s0)处是1阶接触.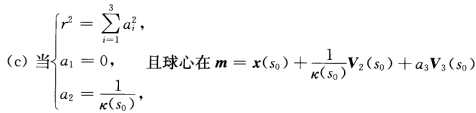 的任何点时x(s)与球面(x一m)2=r2在x(s0)处是2阶接触.
的任何点时x(s)与球面(x一m)2=r2在x(s0)处是2阶接触.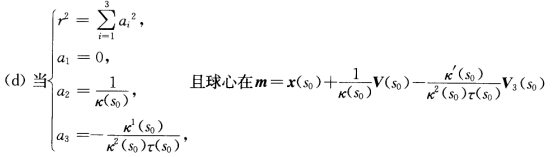 的任何点时x(s0)与球面(x—m)2=r2在x(s0)处是3阶接触.
的任何点时x(s0)与球面(x—m)2=r2在x(s0)处是3阶接触.
证法1(1)设由此知x(s)在x(s0)与球面(x一m)2=r2有2阶接触等价于(2)x(s)在x(s0)与球面(x一m)2=r2有3阶接触等价于此时,证法2设f(s)=[x(s)一m2一r2,m=x(s0)+uV2(s)+tV3(s),则(1)x(s)在s0与球面(x一m)2=r2=u2+t2有2阶接触等价于(2)x(s)在s0与球面(x—m)2=r2=u2+t2有3阶接触等价于由上立知题中所有结论.证法3参阅习题1.3.22证法2,应用Taylor展开.(1)设球面中心为x(s)与球面(x—m)2=r2之间的k阶接触如下:这表明:(a)球心在任何点,只要球面经过x(s0)(即半径r=x(s)与球面(x—m)2=r2在x(s0)处就是0阶接触.(b)当且球心在的任何点时,x(s)与球面(x—m)2=r2在x(s0)处是1阶接触.的任何点时,x(s)与球面(x一m)2=r2在x(s0)处是2阶接触.的任何点时,x(s0)与球面(x—m)2=r2在x(s0)处是3阶接触.
相似问题
X=(x2一y2 一2xy);请帮忙给出正确答案和分析 谢谢!
X=(x2一y2,一2xy);请帮忙给出正确答案和分析,谢谢!
求抛物线y2=2px(p>0)的渐缩线.请帮忙给出正确答案和分析 谢谢!
求抛物线y2=2px(p>0)的渐缩线.请帮忙给出正确答案和分析,谢谢!
两条C3曲线证明:一条C4曲线x(s)为一般螺线等价于(x x x)=(V1 V1 V1)=0.证明
两条C3曲线证明:一条C4曲线x(s)为一般螺线等价于(x,x,x)=(V1,V1,V1)=0.证明:一条C4曲线x(s)为一般螺线等价于(x,x,x)=(V1,V1,V1)=0.请帮忙给
证明:kτ≠0的常曲率的C4曲线的曲率中心的轨迹是常曲率的.请帮忙给出正确答案和分析 谢谢!
证明:kτ≠0的常曲率的C4曲线的曲率中心的轨迹是常曲率的.请帮忙给出正确答案和分析,谢谢!
对R3中定向光滑的2维闭曲面M 如果设M为R3中的2维紧致 光滑 连通曲面 H为其平均曲率 则其中等
对R3中定向光滑的2维闭曲面M,如果设M为R3中的2维紧致、光滑、连通曲面,H为其平均曲率,则其中等号成设M为R3中的2维紧致、光滑、连通曲面,H为其平均曲












