对R3中定向光滑的2维闭曲面M 如果设M为R3中的2维紧致 光滑 连通曲面 H为其平均曲率 则其中等
对R3中定向光滑的2维闭曲面M,如果设M为R3中的2维紧致、光滑、连通曲面,H为其平均曲率,则其中等号成
设M为R3中的2维紧致、光滑、连通曲面,H为其平均曲率,则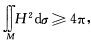 其中等号成立
其中等号成立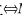 M为一个球面.
M为一个球面.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:设k1k2为曲面M的两个主曲率M+={P∈M|KG(P)≥0)M-={P∈M|KG(P)<0)则有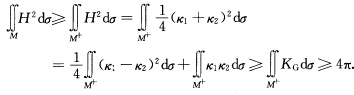 (←)设M为球面则H2=KG≥0M=M+.根据Gauss—Bonnet公式上面式子中各不等号全为等号即有
(←)设M为球面则H2=KG≥0M=M+.根据Gauss—Bonnet公式上面式子中各不等号全为等号即有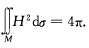 (→)设
(→)设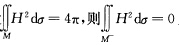 且在M+上k1=k2.根据H2的连续非负知HM-|≡0.从引理3.1.5
且在M+上k1=k2.根据H2的连续非负知HM-|≡0.从引理3.1.5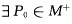 使得KG(P0)>0.由KG的连续性必有P0的连通开邻域UP0使得KG|UP0>0则
使得KG(P0)>0.由KG的连续性必有P0的连通开邻域UP0使得KG|UP0>0则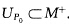 .在UP0上有k1=k2即UP0为全脐的.应用引理3.1.4(1)M|UP0为球面片.在上kP0=k2为非零常数.因为主曲率k1k2连续在UP0上k1=k2=常数≠0所以k1=k2在M上处处成立.因此当
.在UP0上有k1=k2即UP0为全脐的.应用引理3.1.4(1)M|UP0为球面片.在上kP0=k2为非零常数.因为主曲率k1k2连续在UP0上k1=k2=常数≠0所以k1=k2在M上处处成立.因此当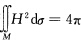 成立时M是紧致、全脐的光滑连通曲面定理3.1。1指出M只能为球面.综合上述有
成立时M是紧致、全脐的光滑连通曲面定理3.1。1指出M只能为球面.综合上述有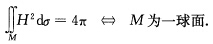
设k1,k2为曲面M的两个主曲率,M+={P∈M|KG(P)≥0),M-={P∈M|KG(P)<0),则有(←)设M为球面,则H2=KG≥0,M=M+.根据Gauss—Bonnet公式,上面式子中各不等号全为等号,即有(→)设且在M+上,k1=k2.根据H2的连续非负知HM-|≡0.从引理3.1.5,,使得KG(P0)>0.由KG的连续性,必有P0的连通开邻域UP0,使得KG|UP0>0,则.在UP0上,有k1=k2,即UP0为全脐的.应用引理3.1.4(1),M|UP0为球面片.在上,kP0=k2为非零常数.因为主曲率k1,k2连续,在UP0上,k1=k2=常数≠0,所以k1=k2在M上处处成立.因此,当成立时,M是紧致、全脐的光滑连通曲面,定理3.1。1指出M只能为球面.综合上述,有
相似问题
证明:曲面M上测地线的方程在一般参数下可取如下形式:请帮忙给出正确答案和分析 谢谢!
证明:曲面M上测地线的方程在一般参数下可取如下形式:请帮忙给出正确答案和分析,谢谢!
X=(x3一3xy2 y3一3x2y).请帮忙给出正确答案和分析 谢谢!
X=(x3一3xy2,y3一3x2y).请帮忙给出正确答案和分析,谢谢!
在下列各题中 求由给定函数复合而成的复合函数。 请帮忙给出正确答案和分析 谢谢!
在下列各题中,求由给定函数复合而成的复合函数。 请帮忙给出正确答案和分析,谢谢!
对R3中定向光滑的2维闭曲面M 如果则M同胚于球面 且它的Gauss曲率KG≥0.请帮忙给出正确答案
对R3中定向光滑的2维闭曲面M,如果则M同胚于球面,且它的Gauss曲率KG≥0.请帮忙给出正确答案和分析,谢谢!
设e1 e2 ω1 ω2和设{r θ}为平面R2上的极坐标系 其参数表示为x=(rcosθ rsin
设e1,e2,ω1,ω2和设{r,θ}为平面R2上的极坐标系,其参数表示为x=(rcosθ,rsinθ).则第1基本形式为I=dr设{r,θ}为平面R2上的极坐标系,其参数表示












