对R3中定向光滑的2维闭曲面M 如果则M同胚于球面 且它的Gauss曲率KG≥0．请帮忙给出正确答案
对R3中定向光滑的2维闭曲面M，如果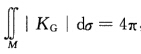
则M同胚于球面，且它的Gauss曲率KG≥0．
请帮忙给出正确答案和分析，谢谢！
参考解答
413***102
2024-11-17 01:17:19
正确答案：由于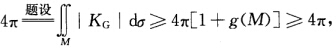
故等号成立必有g(M)=0即X(M)=2[1一g(M)=2．根据R3中2维定向、紧致曲面的拓扑分类定理知M同胚于球面．由
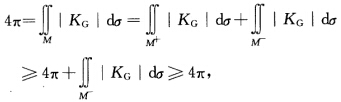立知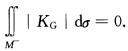
因为｜KG｜在M上连续且非负所以｜KG｜在M-上恒为0即KG在M-上恒为0．从而M-={P∈M｜KG(P)<0)=∮．由此推得在M上KG≥0．
由于故等号成立,必有g(M)=0,即X(M)=2[1一g(M)=2．根据R3中2维定向、紧致曲面的拓扑分类定理,知M同胚于球面．由立知因为｜KG｜在M上连续且非负,所以｜KG｜在M-上恒为0,即KG在M-上恒为0．从而,M-={P∈M｜KG(P)<0)=∮．由此推得,在M上,KG≥0．
相似问题
设e1 e2 ω1 ω2和设{r θ}为平面R2上的极坐标系 其参数表示为x=(rcosθ rsin
设e1，e2，ω1，ω2和设{r，θ}为平面R2上的极坐标系，其参数表示为x=(rcosθ，rsinθ)．则第1基本形式为I=dr设{r，θ}为平面R2上的极坐标系，其参数表示
R3中 设曲线C在曲面M上曲率恒为0或者曲率处处不为0 则曲线C为渐近曲线C为直线或者C的密切平面与
R3中，设曲线C在曲面M上曲率恒为0或者曲率处处不为0，则曲线C为渐近曲线C为直线或者C的密切平面与曲面的切平面重合．请帮忙给出正确答案和分析，谢谢！
设e1 e2 ω1 ω2和为R3中C2超曲面M上的规范正交标架 f为M上的C2函数 (f沿ei方向的
设e1，e2，ω1，ω2和为R3中C2超曲面M上的规范正交标架，f为M上的C2函数，(f沿ei方向的方向导数eif=df(ei)=(f1ω1+f2ω2)(ei)=fi)．记则：(1)；(7)f12=f2
求曲面xyz=a3(a>0)的脐点．请帮忙给出正确答案和分析 谢谢！
求曲面xyz=a3(a>0)的脐点．请帮忙给出正确答案和分析，谢谢！
求曲面的两参数曲线的二等分轨线的微分方程．请帮忙给出正确答案和分析 谢谢！
求曲面的两参数曲线的二等分轨线的微分方程．请帮忙给出正确答案和分析，谢谢！
