设e1 e2 ω1 ω2和为R3中C2超曲面M上的规范正交标架 f为M上的C2函数 (f沿ei方向的
设e1，e2，ω1，ω2和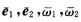
为R3中C2超曲面M上的规范正交标架，f为M上的C2函数，
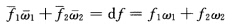(f沿ei方向的方向导数eif=df(ei)=(f1ω1+f2ω2)(ei)=fi)．记
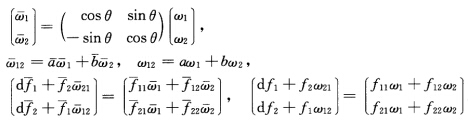则：(1)
；
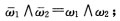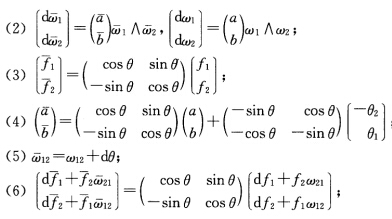(7)f12=f21； (8)f11+f22与规范正交标架的选取无关，并称△1：C2(M，R)→C0(M，R)f1→△1f=f11+f22为M上的Laplace算子．如果△1f=0，则称f为调和函数．
请帮忙给出正确答案和分析，谢谢！
参考解答
420***102
2024-11-17 01:18:42
正确答案：
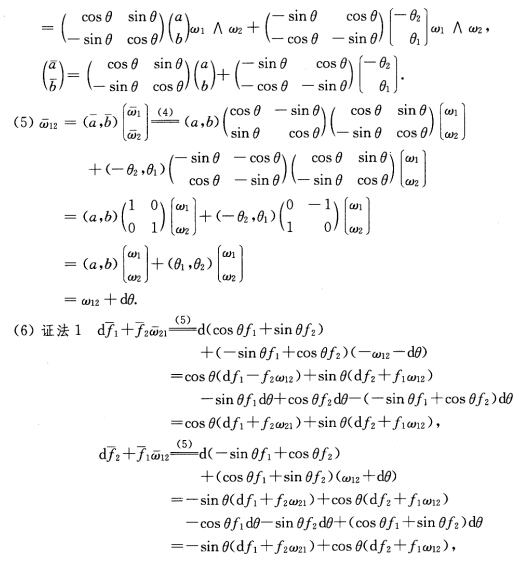
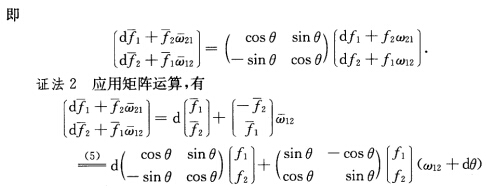
这表明f11+f22与规范正交标架的选取无关．证法2设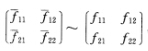
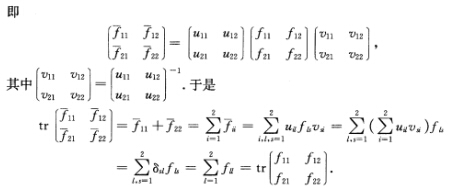
这表明f11+f22与规范正交标架的选取无关．证法2设
相似问题
求曲面xyz=a3(a>0)的脐点．请帮忙给出正确答案和分析 谢谢！
求曲面xyz=a3(a>0)的脐点．请帮忙给出正确答案和分析，谢谢！
求曲面的两参数曲线的二等分轨线的微分方程．请帮忙给出正确答案和分析 谢谢！
求曲面的两参数曲线的二等分轨线的微分方程．请帮忙给出正确答案和分析，谢谢！
求曲面M：z=axy(a>0)上两坐标曲线x=x0与y=y0之间的夹角．请帮忙给出正确答案和分析 谢
求曲面M：z=axy(a>0)上两坐标曲线x=x0与y=y0之间的夹角．请帮忙给出正确答案和分析，谢谢！
设曲面M的第3基本形式为Ⅲ=edu2＋2fdudv＋gdv2． 证明： (1)曲面M的一个双曲点P处
设曲面M的第3基本形式为Ⅲ=edu2＋2fdudv＋gdv2． 证明： (1)曲面M的一个双曲点P处，在曲率不为零的渐曲面M的一个双曲点P处，在曲率不为零的渐近曲线上
证明：在球面上 任何曲线的测地曲率可写成 其中θ表示曲线与经线的交角 s为曲线x(u(s) v(s)
证明：在球面上，任何曲线的测地曲率可写成 其中θ表示曲线与经线的交角，s为曲线x(u(s)，v(s))的弧长参数．再求球面上纬圆的测地曲率(见习题2．8．4图)
