设e1 e2 ω1 ω2和设{r θ}为平面R2上的极坐标系 其参数表示为x=(rcosθ rsin
设e1,e2,ω1,ω2和设{r,θ}为平面R2上的极坐标系,其参数表示为x=(rcosθ,rsinθ).则第1基本形式为I=dr
设{r,θ}为平面R2上的极坐标系,其参数表示为x=(rcosθ,rsinθ).则第1基本形式为I=dr2+r2dθ2,且在极坐标系下,Laplace算子为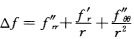 其中f为r,θ的C2函数.
其中f为r,θ的C2函数.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:证法1计算得xr'=(cosθsinθ)x'=(一rsinθrcosθ)E=xr'.xr'=cos2θ+sin2θ=1F=xr'.xθ'=一rcosθsinθ+rsinθcosθ=0 (即xr'⊥xθ')G=xθ'.xθ'=r2sin2θ+r2cos2θ=r2I=Edr2+2Fdrdθ+Gdθ2一dr2+r2dθ2.取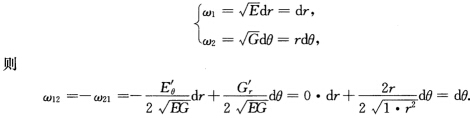 于是对C2函数f
于是对C2函数f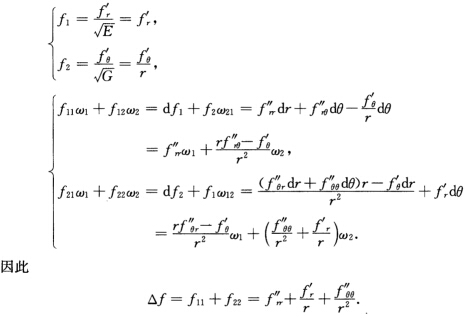 证法2根据习题3.2.3的证法2有
证法2根据习题3.2.3的证法2有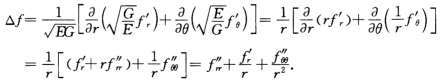
证法1计算得xr'=(cosθ,sinθ),x'=(一rsinθ,rcosθ),E=xr'.xr'=cos2θ+sin2θ=1,F=xr'.xθ'=一rcosθsinθ+rsinθcosθ=0(即xr'⊥xθ'),G=xθ'.xθ'=r2sin2θ+r2cos2θ=r2,I=Edr2+2Fdrdθ+Gdθ2一dr2+r2dθ2.取于是,对C2函数f,证法2根据习题3.2.3的证法2,有
相似问题
R3中 设曲线C在曲面M上曲率恒为0或者曲率处处不为0 则曲线C为渐近曲线C为直线或者C的密切平面与
R3中,设曲线C在曲面M上曲率恒为0或者曲率处处不为0,则曲线C为渐近曲线C为直线或者C的密切平面与曲面的切平面重合.请帮忙给出正确答案和分析,谢谢!
设e1 e2 ω1 ω2和为R3中C2超曲面M上的规范正交标架 f为M上的C2函数 (f沿ei方向的
设e1,e2,ω1,ω2和为R3中C2超曲面M上的规范正交标架,f为M上的C2函数,(f沿ei方向的方向导数eif=df(ei)=(f1ω1+f2ω2)(ei)=fi).记则:(1);(7)f12=f2
求曲面xyz=a3(a>0)的脐点.请帮忙给出正确答案和分析 谢谢!
求曲面xyz=a3(a>0)的脐点.请帮忙给出正确答案和分析,谢谢!
求曲面的两参数曲线的二等分轨线的微分方程.请帮忙给出正确答案和分析 谢谢!
求曲面的两参数曲线的二等分轨线的微分方程.请帮忙给出正确答案和分析,谢谢!
求曲面M:z=axy(a>0)上两坐标曲线x=x0与y=y0之间的夹角.请帮忙给出正确答案和分析 谢
求曲面M:z=axy(a>0)上两坐标曲线x=x0与y=y0之间的夹角.请帮忙给出正确答案和分析,谢谢!












