设f(x)为Rn上的一个Cr函数(r≥1) M={x∈Rn｜f(x)=0}≠∮ 且对 证明：M为一个
设f(x)为Rn上的一个Cr函数(r≥1)，M={x∈Rn｜f(x)=0}≠∮，且对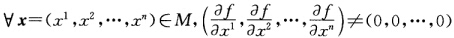
证明：M为一个n一1维Cr微分流形．
请帮忙给出正确答案和分析，谢谢！
参考解答
420***102
2024-11-17 00:13:34
正确答案：对
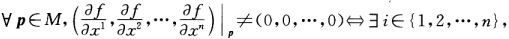使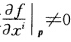
根据隐射(隐函数)定理(参阅[8第103页定理8．4．1)存在p在M上的开邻域Up使得xi=xi(x1x2…xi-1xi+1…xn)为Cr函数．此时{x1x2…xi-1xi+1…xn为Up的局部坐标
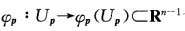φp(x)=(x1x2…xi-1xi+1…xn)为局部坐标映射．于是
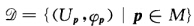确定了M为一个n一1维Cr流形．
对使根据隐射(隐函数)定理(参阅[8第103页定理8．4．1),存在p在M上的开邻域Up,使得xi=xi(x1,x2,…,xi-1,xi+1,…,xn)为Cr函数．此时,{x1,x2,…,xi-1,xi+1,…,xn为Up的局部坐标,,φp(x)=(x1,x2,…,xi-1,xi+1,…,xn)为局部坐标映射．于是确定了M为一个n一1维Cr流形．
相似问题
证明：负常Gauss(总)曲率曲面设曲面M上以点P为中心 r为半径的测地圆的周长为L(r) 所围区域
证明：负常Gauss(总)曲率曲面设曲面M上以点P为中心、r为半径的测地圆的周长为L(r)，所围区域的面积设曲面M上以点P为中心、r为半径的测地圆的周长为L(r)，
设两条曲率大于0的C2曲线之间可建立(可微的)一一对应 使对应点切线处处相同．问：两曲线重合吗?请帮
设两条曲率大于0的C2曲线之间可建立(可微的)一一对应，使对应点切线处处相同．问：两曲线重合吗?请帮忙给出正确答案和分析，谢谢！
证明：当R3中曲面M的参数曲线取曲率线网时 Codazzi方程化为Lv=HEv Nu=HGu．从而再
证明：当R3中曲面M的参数曲线取曲率线网时，Codazzi方程化为Lv=HEv，Nu=HGu．从而再证明：平均曲率为常数的连通曲面为平面片，或者为球面片，或者第1、第
设曲面M：x(u v)=(ucosv usinv lnu)与设M为R3中2维光滑曲面 {u v}为点
设曲面M：x(u，v)=(ucosv，usinv，lnu)与设M为R3中2维光滑曲面，{u，v}为点P∈M邻近的局部坐标(参数)，{x设M为R3中2维光滑曲面，{u，v}为点P∈M邻近的局
证明：(1)证明：正螺面M：x(u v)=(vcosu vsinu bu) (0≤u≤2π 一∞
证明：(1)证明：正螺面M：x(u，v)=(vcosu，vsinu，bu) (0≤u≤2π，一∞<v<＋∞)的渐近曲线就是它上面证明：正螺面M：x(u，v)=(vcosu，vsinu，bu) (0≤
