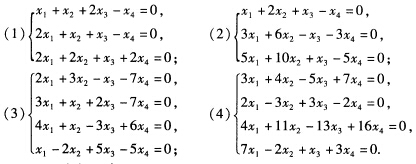参考解答
413***101
2024-11-11 17:04:23
正确答案：(1)对系数矩阵A施以初等行变换化为行最简形矩阵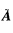
：
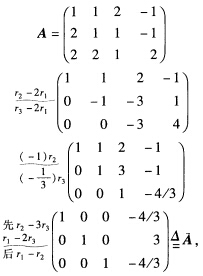即得与原方程组同解的方程组
令x4=c将其解写成通常的参数形式：
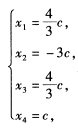其中c为任意实数．或写成向量形式：
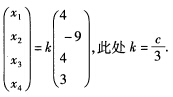(2)对系数矩阵A施以初等行变换化为行最简形矩阵
：
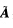即得与原方程组同解的方程组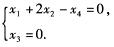
由此即得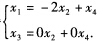
令x2=cx4=c2将其解写成通常的参数形式：
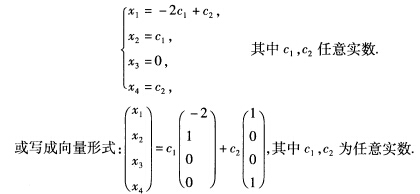(3)对系数矩阵A施以初等行变换化为行阶梯形矩阵：
由最后的行阶梯形矩阵来看R(A)=3故原方程组有解．即得与原方程组同解的方程组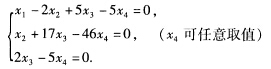
令x4=c把它写成通常的常数形式：
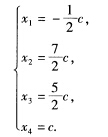其中c为任意实数或写成向量形式：
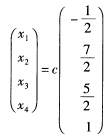(4)对系数矩阵A施以初等行变换化为行阶梯形矩阵：
由上式最后的行阶梯形矩阵看出R(A)=2故原齐次线性方程组有非零解于是可继续施以初等行变换化为行最简形矩阵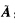
：
(1)对系数矩阵A施以初等行变换,化为行最简形矩阵：即得与原方程组同解的方程组令x4=c,将其解写成通常的参数形式：其中c为任意实数．或写成向量形式：(2)对系数矩阵A施以初等行变换,化为行最简形矩阵：即得与原方程组同解的方程组由此即得令x2=c,x4=c2,将其解写成通常的参数形式：(3)对系数矩阵A施以初等行变换,化为行阶梯形矩阵：由最后的行阶梯形矩阵来看,R(A)=3,故原方程组有解．即得与原方程组同解的方程组令x4=c,把它写成通常的常数形式：其中c为任意实数或写成向量形式：(4)对系数矩阵A施以初等行变换,化为行阶梯形矩阵：由上式最后的行阶梯形矩阵看出R(A)=2,故原齐次线性方程组有非零解,于是可继续施以初等行变换,化为行最简形矩阵：
相似问题
设A∈Rn×n为正矩阵 证明存在唯一向量x 使得Ax=r(A)x x=(x1 x2 … xn)>0及
设A∈Rn×n为正矩阵，证明存在唯一向量x，使得Ax=r(A)x，x=(x1，x2，…，xn)>0及请帮忙给出正确答案和分析，谢谢！
一个质点沿光滑的抛物线轨道 从初始位置(2．2)无初速地滑下 如图1—17所示 求质点在何处离开抛物
一个质点沿光滑的抛物线轨道，从初始位置(2．2)无初速地滑下，如图1—17所示，求质点在何处离开抛物线轨道?抛物线为y2=2x的上枝，y沿重力的反向，式中x，
以下关于船舶拖航的表述 符合我国《海商法》规定的有( )A 海上拖航合同应当书面订立B 在港区内对船
以下关于船舶拖航的表述，符合我国《海商法》规定的有( )A、海上拖航合同应当书面订立B、在港区内对船舶提供的拖轮服务不适用《海商法》C、承拖方在起拖
如图1一12所示 在地球纬度为α地面的垂直方向上 质量为m 长为l的摆 以角频率振动着 地球自转的角
如图1一12所示，在地球纬度为α地面的垂直方向上，质量为m，长为l的摆，以角频率振动着，地球自转的角速度为Ω。则摆的振动面转动的周期为 请帮忙给出正
设A为m×n矩阵 证明：方程Ax=Em有解的充要条件为R(A)=m．请帮忙给出正确答案和分析 谢谢！
设A为m×n矩阵，证明：方程Ax=Em有解的充要条件为R(A)=m．请帮忙给出正确答案和分析，谢谢！
