有一均匀的球体 球心在原点 在球面上温度为u|r=a=u0cosθ(1-cosθ)试在稳定状态下 就
有一均匀的球体,球心在原点,在球面上温度为u|r=a=u0cosθ(1-cosθ)试在稳定状态下,就边界条件求球内的温度分布。
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:即所求问题为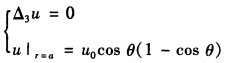 因为是球内问题所求有限解形式为
因为是球内问题所求有限解形式为 因为边界条件与φ无关所以其解也与φ无关即
因为边界条件与φ无关所以其解也与φ无关即
即所求问题为因为是球内问题,所求有限解形式为因为边界条件与φ无关,所以其解也与φ无关,即
相似问题
设A B皆为非空有界数集 定义数集A+B={z|z=x+y x∈A y∈B}。证明: sup(A+B
设A、B皆为非空有界数集,定义数集A+B={z|z=x+y,x∈A,y∈B}。证明: sup(A+B)=supA+supB请帮忙给出正确答案和分析,谢谢!
设{αn)是无界数列 {bn}是无穷大数列.证明:{αnbn}必为无界数列。请帮忙给出正确答案和分析
设{αn)是无界数列,{bn}是无穷大数列.证明:{αnbn}必为无界数列。请帮忙给出正确答案和分析,谢谢!
内半径为a 外半径为b的薄圆环面均匀带点 其总电量为4πε0Q 将球坐标系的原点取在环心 极轴垂直于
内半径为a,外半径为b的薄圆环面均匀带点,其总电量为4πε0Q,将球坐标系的原点取在环心,极轴垂直于环面,求空间各点的电势。提示:v(r,θ)|θ=0=v(r
设α为有理数 x为无理数 证明: (1)α+x是无理数; (2)当α≠0时 αx是无理数。请帮忙给出
设α为有理数,x为无理数,证明: (1)α+x是无理数; (2)当α≠0时,αx是无理数。请帮忙给出正确答案和分析,谢谢!
设函数f(x)在区间I上连续 证明: (1)若对任何有理数r∈I有f(r)=0 则在I上f(x)=0
设函数f(x)在区间I上连续,证明: (1)若对任何有理数r∈I有f(r)=0,则在I上f(x)=0; (2)若对任意两个有理数r1,r2,r1<r2,有f(r1)<f(r2),则f(x)在I












