在x=0点的邻域求解常微分方程y'+ω2y=0 ①请帮忙给出正确答案和分析 谢谢！
在x=0点的邻域求解常微分方程y"+ω2y=0 ①
请帮忙给出正确答案和分析，谢谢！
参考解答
490***102
2024-11-18 00:22:41
正确答案：可知此处P(x)=0q(x)=ω2在x=0均解析故x=0为该方程的常点。由题令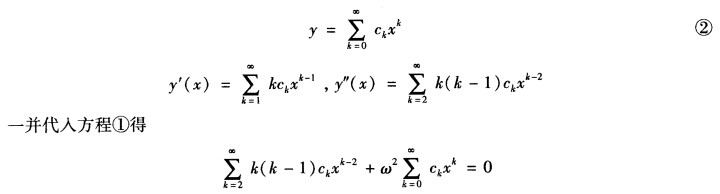
由于上式对x是一个恒等式故左边x的各次幂的系数必须为零。即 x0的系数：2.1c2+ω2c0=0 x1的系数：3.2c3+ω2c1=0xk的系数：(k+2)(k+1)ck+2+ω2ck=0
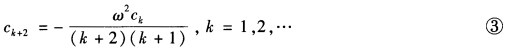由上可看出由xk的系数ck便可算出xk+2的系数ck+2故称以上公式为系数递推公式。由式③可具体推得 
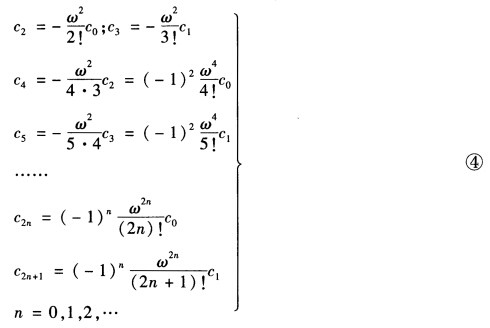将式④代入式②得方程①的解为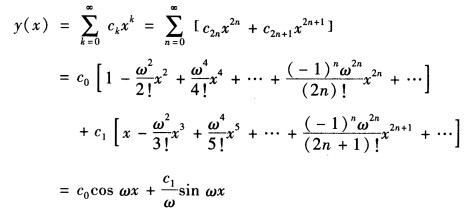
可知,此处P(x)=0,q(x)=ω2在x=0均解析,故x=0为该方程的常点。由题令由于上式对x是一个恒等式,故左边x的各次幂的系数必须为零。即x0的系数：2.1c2+ω2c0=0x1的系数：3.2c3+ω2c1=0xk的系数：(k+2)(k+1)ck+2+ω2ck=0由上可看出,由xk的系数ck,便可算出xk+2的系数ck+2,故称以上公式为系数递推公式。由式③可具体推得将式④代入式②,得方程①的解为
相似问题
有一均匀的球体 球心在原点 在球面上温度为u|r=a=u0cosθ(1-cosθ)试在稳定状态下 就
有一均匀的球体，球心在原点，在球面上温度为u|r=a=u0cosθ(1-cosθ)试在稳定状态下，就边界条件求球内的温度分布。请帮忙给出正确答案和分析，谢谢！
设A B皆为非空有界数集 定义数集A+B={z｜z=x+y x∈A y∈B}。证明： sup(A+B
设A、B皆为非空有界数集，定义数集A+B={z｜z=x+y，x∈A，y∈B}。证明： sup(A+B)=supA+supB请帮忙给出正确答案和分析，谢谢！
设{αn)是无界数列 {bn}是无穷大数列．证明：{αnbn}必为无界数列。请帮忙给出正确答案和分析
设{αn)是无界数列，{bn}是无穷大数列．证明：{αnbn}必为无界数列。请帮忙给出正确答案和分析，谢谢！
内半径为a 外半径为b的薄圆环面均匀带点 其总电量为4πε0Q 将球坐标系的原点取在环心 极轴垂直于
内半径为a，外半径为b的薄圆环面均匀带点，其总电量为4πε0Q，将球坐标系的原点取在环心，极轴垂直于环面，求空间各点的电势。提示：v(r，θ)|θ=0=v(r
设α为有理数 x为无理数 证明： (1)α+x是无理数； (2)当α≠0时 αx是无理数。请帮忙给出
设α为有理数，x为无理数，证明： (1)α+x是无理数； (2)当α≠0时，αx是无理数。请帮忙给出正确答案和分析，谢谢！
