讨论下列幂级数的敛散性： (1)； (2)请帮忙给出正确答案和分析 谢谢！
讨论下列幂级数的敛散性： (1)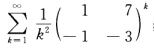
； (2)
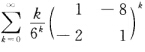
请帮忙给出正确答案和分析，谢谢！
参考解答
406***101
2024-11-12 00:01:02
正确答案：(1)设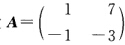
可求得A的特征值为λ1=λ2=－2所以γ(A)=2．幂级数
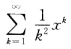的收敛半径为
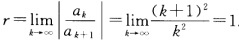由γ(A)=2>γ知矩阵幂级数
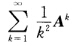发散． (2)设
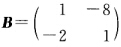可求得B的特征值为λ1=－3λ2=5所以γ(B)=5．又因为幂级数
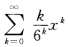的收敛半径为
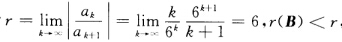γ(B)<γ所以矩阵幂级数
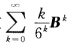绝对收敛．
(1)设,可求得A的特征值为λ1=λ2=－2,所以γ(A)=2．幂级数的收敛半径为由γ(A)=2>γ知,矩阵幂级数发散．(2)设,可求得B的特征值为λ1=－3,λ2=5,所以γ(B)=5．又因为幂级数的收敛半径为,γ(B)<γ,所以矩阵幂级数绝对收敛．
相似问题
设A B∈Cn×n AB=BA 证明： sin(A+B)=sin Acos B+cos Asin B
设A，B∈Cn×n，AB=BA，证明： sin(A+B)=sin Acos B+cos Asin B，cos(A+B)=cos Acos B－sin Asin B．请帮忙给出正确答案和分析，谢谢！
求矩阵A=的奇异值分解．请帮忙给出正确答案和分析 谢谢！
求矩阵A=的奇异值分解．请帮忙给出正确答案和分析，谢谢！
若∥.∥是算子范数 则 (1)∥E∥=1； (2)∥A－1∥≥∥A∥－1； (3)请帮忙给出正确答案
若∥ ∥是算子范数，则 (1)∥E∥=1； (2)∥A－1∥≥∥A∥－1； (3)请帮忙给出正确答案和分析，谢谢！
设∥A∥v ∥A∥μ是对应于两个向量范数∥x∥v ∥x∥μ=∥Bx∥v的算子范数 B可逆 则∥A∥μ
设∥A∥v，∥A∥μ是对应于两个向量范数∥x∥v，∥x∥μ=∥Bx∥v的算子范数，B可逆，则∥A∥μ=∥BAB－1∥v请帮忙给出正确答案和分析，谢谢！
证明：0m×n的自反广义逆矩阵仅为0n×m．请帮忙给出正确答案和分析 谢谢！
证明：0m×n的自反广义逆矩阵仅为0n×m．请帮忙给出正确答案和分析，谢谢！
