计算悬链面M：设曲面M的第1基本形式为I=du2＋(u2＋a2)dv2．求出曲面M上由三条曲线u＋a

大学本科已帮助：人时间:2024-11-17 00:28:24

计算悬链面M：设曲面M的第1基本形式为I=du2＋(u2＋a2)dv2．求出曲面M上由三条曲线u＋av(a＞0)，v=1相交
设曲面M的第1基本形式为I=du2+(u2+a2)dv2．求出曲面M上由三条曲线u+av(a＞0)，v=1相交所成的三角形的面积A
请帮忙给出正确答案和分析，谢谢！

4j8***102

2024-11-17 00:28:24



正确答案：由I=Edu²+2Fdudv+Gdv²=du²+(u²+a²)dv²知E=1 F=0 G=u²+a²所以(记此三角形为△)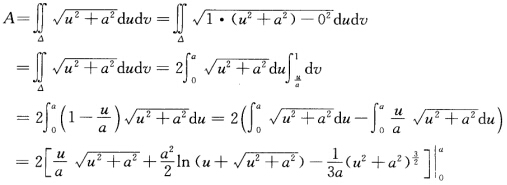
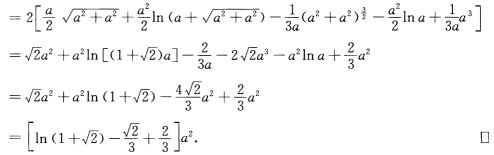
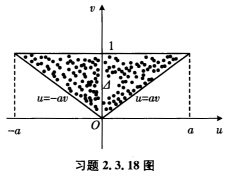
由I=Edu2+2Fdudv+Gdv2=du2+(u2+a2)dv2,知E=1,F=0,G=u2+a2,所以(记此三角形为△)

求圆的一条渐伸线．请帮忙给出正确答案和分析谢谢！

求圆的一条渐伸线．请帮忙给出正确答案和分析，谢谢！
验证：M6bius带M：为直纹面．它是可展曲面吗?请帮忙给出正确答案和分析谢谢！

验证：M6bius带M：为直纹面．它是可展曲面吗?请帮忙给出正确答案和分析，谢谢！
证明：k>0的曲线为曲面上的测地线曲线的密切平面与曲面的切平面正交(即V3⊥n)由V1 V2张成的

证明：k>0的曲线为曲面上的测地线曲线的密切平面与曲面的切平面正交(即V3⊥n)由V1，V2张成的从切平面与切平面重合(即V2∥n)．请帮忙给出正确答案和分析，谢谢！
求Iijk；请帮忙给出正确答案和分析谢谢！

求Iijk；请帮忙给出正确答案和分析，谢谢！
旋轮线(摆线)：x(t)=a(t—sint 1-cost)；请帮忙给出正确答案和分析谢谢！

旋轮线(摆线)：x(t)=a(t—sint，1-cost)；请帮忙给出正确答案和分析，谢谢！

求圆的一条渐伸线．请帮忙给出正确答案和分析谢谢！