证明：直纹面M的Gauss(总)曲率不可能为正 即KG≤0．请帮忙给出正确答案和分析 谢谢！

正确答案：(反证)假设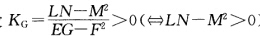根据定义2．4．3知Ldu²+2Mdudv+Ndv²=0的判别式△=(2M)²一4LN=4(M²一LN)(0故直纹面M无实的渐近方向这与直纹面M上直母线为渐近曲线相矛盾．因此K_G≤0．证法2沿着直母线(渐近方向)0=k_n=k₁cos²θ+k₂sin²θ故k₁k₂不能同为正或同为负．从而K_G=k₁k₂≤0．证法3设直纹面方程为x(uv)=a(u)+vl(u)．根据例2．3．4知N=0故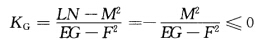
(反证)假设根据定义2．4．3,知Ldu2+2Mdudv+Ndv2=0的判别式△=(2M)2一4LN=4(M2一LN)(0,故直纹面M无实的渐近方向,这与直纹面M上直母线为渐近曲线相矛盾．因此,KG≤0．证法2沿着直母线(渐近方向),0=kn=k1cos2θ+k2sin2θ,故k1,k2不能同为正或同为负．从而KG=k1k2≤0．证法3设直纹面方程为x(u,v)=a(u)+vl(u)．根据例2．3．4,知N=0,故