验证：M6bius带M： 为直纹面．它是可展曲面吗?请帮忙给出正确答案和分析 谢谢！
验证：M6bius带M：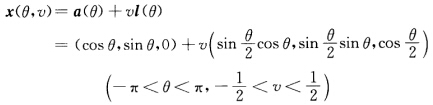 
为直纹面．它是可展曲面吗?
请帮忙给出正确答案和分析，谢谢！
参考解答
490***102
2024-11-17 00:27:29
正确答案：因为固定θ时x(θv)=a(θ)+vl(θ)是过点a(θ)、以l(θ)为方向的直线所以M6bius带M为直纹面．又因为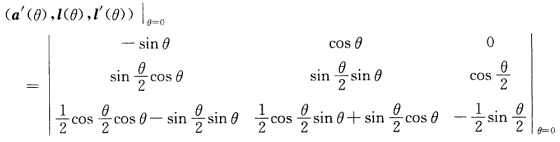
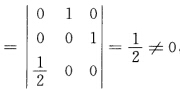故根据定理2．2．1知Mobius带M不是可展曲面．
因为固定θ时,x(θ,v)=a(θ)+vl(θ)是过点a(θ)、以l(θ)为方向的直线,所以M6bius带M为直纹面．又因为故根据定理2．2．1知,Mobius带M不是可展曲面．
相似问题
证明：k>0的曲线为曲面上的测地线 曲线的密切平面与曲面的切平面正交(即V3⊥n)由V1 V2张成的
证明：k>0的曲线为曲面上的测地线 曲线的密切平面与曲面的切平面正交(即V3⊥n)由V1，V2张成的从切平面与切平面重合(即V2∥n)．请帮忙给出正确答案和分析，谢谢！
求Iijk；请帮忙给出正确答案和分析 谢谢！
求Iijk；请帮忙给出正确答案和分析，谢谢！
旋轮线(摆线)：x(t)=a(t—sint 1-cost)；请帮忙给出正确答案和分析 谢谢！
旋轮线(摆线)：x(t)=a(t—sint，1-cost)；请帮忙给出正确答案和分析，谢谢！
设f(x)为Rn上的一个Cr函数(r≥1) M={x∈Rn｜f(x)=0}≠∮ 且对 证明：M为一个
设f(x)为Rn上的一个Cr函数(r≥1)，M={x∈Rn｜f(x)=0}≠∮，且对 证明：M为一个n一1维Cr微分流形．请帮忙给出正确答案和分析，谢谢！
证明：负常Gauss(总)曲率曲面设曲面M上以点P为中心 r为半径的测地圆的周长为L(r) 所围区域
证明：负常Gauss(总)曲率曲面设曲面M上以点P为中心、r为半径的测地圆的周长为L(r)，所围区域的面积设曲面M上以点P为中心、r为半径的测地圆的周长为L(r)，
