设物体A从点(0 1)出发 以速度大小为常数v沿y轴正向运动 物体B从点(－1 0)与A同时出发 其

参考解答

4j8***101

2024-11-09 12:36:36



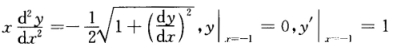相似问题

• 设对任意x＞0 曲线y＝f(x)上的点(x f(x))处的切线在y轴上的截距等于 求f(x)的一般表

  设对任意x＞0，曲线y＝f(x)上的点(x，f(x))处的切线在y轴上的截距等于，求f(x)的一般表达式．请帮忙给出正确答案和分析，谢谢！

• 用常数变易法求下列线性微分方程的通解: (1)y〞＋y＝secx 已知y1(x)＝cosx是方程y〞

  用常数变易法求下列线性微分方程的通解: (1)y〞＋y＝secx，已知y1(x)＝cosx是方程y〞＋y＝0的一个解； (2)(2x－1)y〞－(2x＋1)yˊ＋2y＝0，已知y1(x)＝

• 设y＝y(x)是一向上凸的连续曲线 其上任意一点(x y)处的曲率为 且此曲线上点(0 1)处的切线

  设y＝y(x)是一向上凸的连续曲线，其上任意一点(x，y)处的曲率为，且此曲线上点(0，1)处的切线方程为y＝x＋1，求该曲线的方程，并求函数y＝y(x)的极值．请

• 设f(x) g(x)在区间[－a a](a＞0)上连续 g(x)为偶函数 且f(x)满足条件f(x)

  设f(x)，g(x)在区间[－a，a](a＞0)上连续，g(x)为偶函数，且f(x)满足条件f(x)＋f(－x)＝A(A为常数)． (1)证明∫－aaf(x)g(x)dx＝A∫0ag(x)dx； (2)利用

• 在某一人群中推广新技术是通过其中已掌握新技术的人进行的 设该人群的总人数为N 在t＝0时刻已掌握新技

  在某一人群中推广新技术是通过其中已掌握新技术的人进行的，设该人群的总人数为N，在t＝0时刻已掌握新技术的人数为xo，在任意时刻t已掌握新技术的人数为x