设y＝y(x)是一向上凸的连续曲线 其上任意一点(x y)处的曲率为 且此曲线上点(0 1)处的切线
设y＝y(x)是一向上凸的连续曲线，其上任意一点(x，y)处的曲率为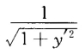
，且此曲线上点(0，1)处的切线方程为y＝x＋1，求该曲线的方程，并求函数y＝y(x)的极值．
请帮忙给出正确答案和分析，谢谢！
参考解答
413***101
2024-11-09 12:35:35
正确答案：因曲线向上凸故y'＜0又由已知得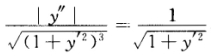
即y”＝－(1＋y’ 2)。由曲线经过点(01)处及切线方程．y＝x＋1可得初始条件y(0)＝1y'(0)＝1．令p＝y'得p'＝－(1＋p2)分离变量并积分得arctanp＝C1—x即 arctany'＝C1－x代入初始条件y(0)＝1y'(0)＝1得
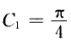有
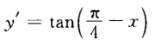两边积分得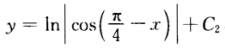
代入条件y(0)＝1得
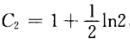所以所求曲线方程为
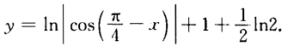因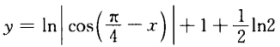
是周期函数故取其含x＝0在内且连续的一支为
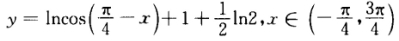当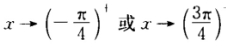
时y→－∞故函数无极小值当
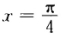时y取到极大值极大值为
。
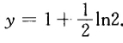[分析由曲率的计算公式和已知条件建立一个二阶微分方程，由曲线经过点(0，1)处及切线方程y＝x＋1，可得初始条件y(0)＝1，y'(0)＝1．[评注本题是一道综合题，主要考查曲率、可降阶微分方程求解及函数的极值问题，综合相关的知识点构造综合题型是考研命题的一大趋势．
相似问题
设f(x) g(x)在区间[－a a](a＞0)上连续 g(x)为偶函数 且f(x)满足条件f(x)
设f(x)，g(x)在区间[－a，a](a＞0)上连续，g(x)为偶函数，且f(x)满足条件f(x)＋f(－x)＝A(A为常数)． (1)证明∫－aaf(x)g(x)dx＝A∫0ag(x)dx； (2)利用
在某一人群中推广新技术是通过其中已掌握新技术的人进行的 设该人群的总人数为N 在t＝0时刻已掌握新技
在某一人群中推广新技术是通过其中已掌握新技术的人进行的，设该人群的总人数为N，在t＝0时刻已掌握新技术的人数为xo，在任意时刻t已掌握新技术的人数为x
三阶常系数线性齐次微分方程y'＝2y'＋y－2y＝0的通解为y＝________．请帮忙给出正确答案
三阶常系数线性齐次微分方程y "＝2y "＋y－2y＝0的通解为y＝________．请帮忙给出正确答案和分析，谢谢！
求下列微分方程的通解: (1)y〞＝xex； (2)(1＋x2)y〞＝1； (3)y〞＋yˊ＝x2；
求下列微分方程的通解: (1)y〞＝xex； (2)(1＋x2)y〞＝1； (3)y〞＋yˊ＝x2； (4)y〞＝1＋yˊ2； (5)x2y〞＝yˊ2＋2xyˊ； (6)(1－y)y〞＋2yˊ2＝0
已知弹簧自然长度为0．6m 10 N的力使它伸长到1m 问使弹簧从0．9m伸长到1m时需要作的功．请
已知弹簧自然长度为0．6m，10 N的力使它伸长到1m，问使弹簧从0．9m伸长到1m时需要作的功．请帮忙给出正确答案和分析，谢谢！
