在xOy坐标平面上 连续曲线 过点M(1 0) 其上任意点P(x y)(x≠0)处的切线斜率与直线O
在xOy坐标平面上，连续曲线，过点M(1，0)，其上任意点P(x，y)(x≠0)处的切线斜率与直线OP的斜牢之差等于ax，(常数a＞0)． (1)求l的方程； (2)当l与直线y＝ax所围成平面图形的而积为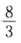
时，确定a的值．
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***101
2024-11-09 13:58:01
正确答案：(1)设曲线的方程为y＝f(x)则由题设可得
这是一阶线性微分方程其中
Q(x)＝ax代入通解公式得
又f(1)＝0＝a＋C所以C＝－a． 故曲线l的方程为y＝ax2－ax． (2)曲线l与直线y＝ax(a＞0)所同成的平面图形如图1—3—11所示．
所以
故 a＝2．
[分析(1)利用导数的几何意义建立微分方程，并求解；(2)利用定积分计算平面图形的面积，确定参数．[评注本题涉及了导数和定积分的几何意义以及一阶线性微分方程的求解，属基本题型．
相似问题
设函数f(x)连续 且 已知f(1)＝1 求∫12f(x)dx的值．请帮忙给出正确答案和分析 谢谢！
设函数f(x)连续，且，已知f(1)＝1，求∫12f(x)dx的值．请帮忙给出正确答案和分析，谢谢！
计算不定积分。请帮忙给出正确答案和分析 谢谢！
计算不定积分。请帮忙给出正确答案和分析，谢谢！
设f(x)连续 则＝_______。请帮忙给出正确答案和分析 谢谢！
设f(x)连续，则＝_______。请帮忙给出正确答案和分析，谢谢！
设函数y＝y(x)由参数方程(t＞1)所确定 求。请帮忙给出正确答案和分析 谢谢！
设函数y＝y(x)由参数方程(t＞1)所确定，求。请帮忙给出正确答案和分析，谢谢！
设f(x)在[0 1]上连续 在(0 1)内可导 且满足 k＞1 证明至少存在一点ξ∈(0 1) 使
设f(x)在[0，1]上连续，在(0，1)内可导，且满足，k＞1，证明至少存在一点ξ∈(0，1)，使得f(ξ)＝(1－ξ－1)f(ξ)．请帮忙给出正确答案和分析，谢谢！
