。参考解答
481***101
2024-11-09 13:58:57
正确答案：[详解1 设x＝tant则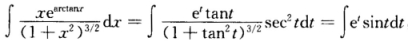 
又 ∫etsintdt＝－∫etdcost＝－(etcost—∫etcostdt) ＝－etcost＋etsint—∫etsintdt故
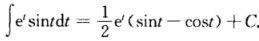。因此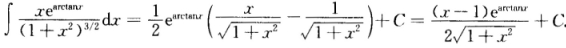
。[详解2 直接用分部积分法：
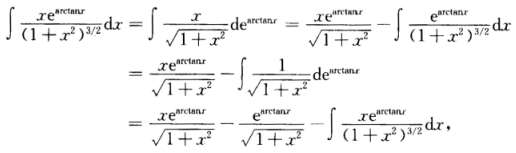移项整理得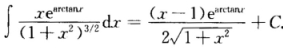
。
[分析被积函数含有根号，应作代换x＝tant，或被积函数含有反三角函数arctanx，同样可考虑作变换arctanx＝t，即x＝tant．[评注本题的关键是含有反三角函数，作代换arctanx＝t或x＝tant．
相似问题
设f(x)连续 则＝_______。请帮忙给出正确答案和分析 谢谢！
设f(x)连续，则＝_______。请帮忙给出正确答案和分析，谢谢！
设函数y＝y(x)由参数方程(t＞1)所确定 求。请帮忙给出正确答案和分析 谢谢！
设函数y＝y(x)由参数方程(t＞1)所确定，求。请帮忙给出正确答案和分析，谢谢！
设f(x)在[0 1]上连续 在(0 1)内可导 且满足 k＞1 证明至少存在一点ξ∈(0 1) 使
设f(x)在[0，1]上连续，在(0，1)内可导，且满足，k＞1，证明至少存在一点ξ∈(0，1)，使得f(ξ)＝(1－ξ－1)f(ξ)．请帮忙给出正确答案和分析，谢谢！
求下列函数的二阶导数： (1)y＝3x2＋e2x＋lnx； (2)y＝xcosx； 请帮忙给出正确答
求下列函数的二阶导数： (1)y＝3x2＋e2x＋lnx； (2)y＝xcosx； 请帮忙给出正确答案和分析，谢谢！
如图1—3—13 曲线段的方程为y＝f(x) 函数f(x)在区间[0 a]上有连续的导数 则定积分∫
如图1—3—13，曲线段的方程为y＝f(x)，函数f(x)在区间[0，a]上有连续的导数，则定积分∫0axf(x)dx等于 A．曲边梯形ABOD的面积．B．梯形ABOD的面积．C．
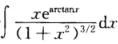