如图1—3—13 曲线段的方程为y=f(x) 函数f(x)在区间[0 a]上有连续的导数 则定积分∫
如图1—3—13,曲线段的方程为y=f(x),函数f(x)在区间[0,a]上有连续的导数,则定积分∫0axf(x)dx等于 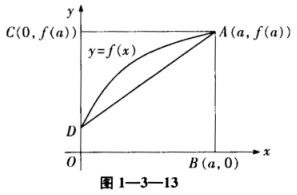
A.曲边梯形ABOD的面积.
B.梯形ABOD的面积.
C.曲边三角形ACD的面积.
D.三角形ACD的面积.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:C
因为∫0axf'(X)dx=∫0axdf(x)=xf(x)|0a-∫0af(x)dx=af(a)-∫0af(x)dx,其中af(a)是矩形ABOC的面积,∫0af(x)dx为曲边梯形ABOD的面积,所以∫0axf'(x)dx为曲边三角形ACD的面积.
相似问题
设函数f(x)在[0 π]上连续 且|f(x)dx=0 |f(x)cosxdx=0 试证明:在(0
设函数f(x)在[0,π]上连续,且|f(x)dx=0,|f(x)cosxdx=0,试证明:在(0,π)内至少存在两个不同的点ξ1,ξ2,使f(ξ1)=f(ξ0)=0.请帮忙给出正确答案和分析,谢谢!
位于曲线y=xex(0≤x<+∞)下方 x轴上方的无界图形的面积是______.请帮忙给出正确答案和
位于曲线y=xex(0≤x<+∞)下方、x轴上方的无界图形的面积是______.请帮忙给出正确答案和分析,谢谢!
微分方程y+y=e-xcosx满足条件y(0)=0的解为_______.请帮忙给出正确答案和分析 谢
微分方程y+y=e-xcosx满足条件y(0)=0的解为_______.请帮忙给出正确答案和分析,谢谢!
设f(x)为正值连接函数 f(0)=1 且对任一x>0 曲线y=f(x)在区间[0 x]上的一段弧长
设f(x)为正值连接函数,f(0)=1,且对任一x>0,曲线y=f(x)在区间[0,x]上的一段弧长等于此弧段下曲边梯形的面积,求此曲线方程.请帮忙给出正确答案和
常压下的液漏时间 有一盛满水的圆锥形漏斗 高为10 cm 顶角为60° 斗下面有一个面积为0.5 c
常压下的液漏时间 有一盛满水的圆锥形漏斗,高为10 cm,顶角为60°,斗下面有一个面积为0.5 cm2的小孔,水从小孔流出(如图4.1所示),由水力学中的托












