过点(0 1)作曲线L:y=lnx的切线 切点为A 又L与x轴交于B点 区域D由L与直线AB围成 求
过点(0,1)作曲线L:y=lnx的切线,切点为A,又L与x轴交于B点,区域D由L与直线AB围成,求区域D的面积及D绕x轴旋转一周所得旋转体的体积.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)如1—3—18设切点A的坐标为(x0y0)则曲线y=lnx在A点处的切线方程为: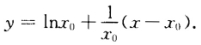 由该切线过点(01)知lnx0-1=1从而x0=e2y0=2.故平面图形D的面积为:
由该切线过点(01)知lnx0-1=1从而x0=e2y0=2.故平面图形D的面积为: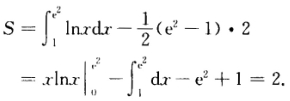 (2)直线AB:
(2)直线AB: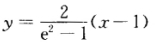 (x—1)与x轴及直线x=e2所围成的三角形绕x轴旋转一周所得圆锥体的体积为
(x—1)与x轴及直线x=e2所围成的三角形绕x轴旋转一周所得圆锥体的体积为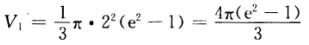 因此D绕x轴旋转一周所得旋转体的体积
因此D绕x轴旋转一周所得旋转体的体积
(1)如1—3—18,设切点A的坐标为(x0,y0),则曲线y=lnx在A点处的切线方程为:由该切线过点(0,1)知lnx0-1=1,从而x0=e2,y0=2.故平面图形D的面积为:(2)直线AB:(x—1)与x轴及直线x=e2所围成的三角形绕x轴旋转一周所得圆锥体的体积为因此,D绕x轴旋转一周所得旋转体的体积
相似问题
设函数f(x)在闭区间[0 1]上连续 在开区间(0 1)内大于零 并满足(a为常数) 又曲线y=f
设函数f(x)在闭区间[0,1]上连续,在开区间(0,1)内大于零,并满足(a为常数),又曲线y=f(x)与x=1,y=0所围的图形S的面积值为2,求函数y=f(x),并问a
设非负函数y=y(x)(x≥0)满足微分方程xy'-y+2=0.当曲线y=y(x)过原点时 其与直线
设非负函数y=y(x)(x≥0)满足微分方程xy"-y+2=0.当曲线y=y(x)过原点时,其与直线x=1及y=0围成的平面区域D的面积为2,求D绕y轴旋转所得旋转体的体
设曲线L的方程为(1≤x≤e). (1)求L的弧长; (2)设D是由曲线L 直线x=1 x=e及x轴
设曲线L的方程为(1≤x≤e). (1)求L的弧长; (2)设D是由曲线L,直线x=1,x=e及x轴所围平面图形,求D的形心的横坐标.请帮忙给出正确答案和分析,谢谢!
如图1—3—12 连续函数y=(x)在区间[-3 -2] [2 3]上的图形分别是直径为1的上 下半
如图1—3—12,连续函数y=(x)在区间[-3,-2],[2,3]上的图形分别是直径为1的上、下半圆周,在区间[-2,0],[0,2]上的图形分别是直径为2的下、上半
设函数f(x)与g(x)在[0 1]上连续 且f(x)≤g(x) 且对任何c∈(0 1)A..B..
设函数f(x)与g(x)在[0,1]上连续,且f(x)≤g(x),且对任何c∈(0,1)A..B..C..D..请帮忙给出正确答案和分析,谢谢!












