如图1—3—12 连续函数y＝(x)在区间[－3 －2] [2 3]上的图形分别是直径为1的上 下半
如图1—3—12，连续函数y＝(x)在区间[－3，－2]，[2，3]上的图形分别是直径为1的上、下半圆周，在区间[－2，0]，[0，2]上的图形分别是直径为2的下、上半圆周．设F(x)＝∫0xf(t)dt出，则下列结论正确的是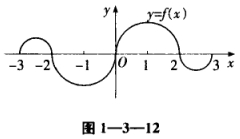 
A．F(3)＝－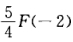
B．F(3)＝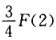
C．F(－3)＝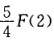
D．F(－3)＝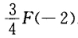
请帮忙给出正确答案和分析，谢谢！
参考解答
456***101
2024-11-09 15:15:04
正确答案：C
[分析本题考查定积分的几何意义，应注意f(x)在不同区间段上的符号，从而搞清楚相应积分与面积的关系．[详解根据定积分的几何意义，F(2)和F(－2)相等：，F(－2)＝∫02f(x)dx＝∫0－2－f(x)dx；F(－3)＝F(3)，F(3)是两个半圆面积之差，F(3)＝，同样，F(－3)＝∫0－3f(x)dx∫－30－f(x)dx＝，故应选(C)．[评注若直接去计算定积分，则本题的计算将十分复杂，而这正是本题设计的巧妙之处．
相似问题
设函数f(x)与g(x)在[0 1]上连续 且f(x)≤g(x) 且对任何c∈(0 1)A．．B．．
设函数f(x)与g(x)在[0，1]上连续，且f(x)≤g(x)，且对任何c∈(0，1)A．．B．．C．．D．．请帮忙给出正确答案和分析，谢谢！
求定积分∫－11(2x＋｜x｜＋1)2dx．请帮忙给出正确答案和分析 谢谢！
求定积分∫－11(2x＋｜x｜＋1)2dx．请帮忙给出正确答案和分析，谢谢！
设Ik＝∫0kπex2sinxdx(k＝1 2 3) 则有A．I1＜I2＜I3．B．I3＜I2＜I1
设Ik＝∫0kπex2sinxdx(k＝1，2，3)，则有A．I1＜I2＜I3．B．I3＜I2＜I1．C．I2＜I3＜I1．D．I2＜I1＜I3．请帮忙给出正确答案和分析，谢谢！
设函数f(x)连续 ψ(x)＝∫01f(xt)dt 且(A为常数) 求ψ(x) 并讨论ψ(x)在x＝
设函数f(x)连续，ψ(x)＝∫01f(xt)dt，且(A为常数)，求ψ(x)，并讨论ψ(x)在x＝0处的连续性．请帮忙给出正确答案和分析，谢谢！
设水以常速(即单位时间注入的水的体积为常数)注入图2．7所示的罐中 直至将水罐注满． 画出水位高度随
设水以常速(即单位时间注入的水的体积为常数)注入图2．7所示的罐中，直至将水罐注满． 画出水位高度随时问变化的函数y＝y(t)的图形(不要求精确图形，但
