设矩阵A=矩阵X满足AX+E=A2+X 试求矩阵X.请帮忙给出正确答案和分析 谢谢!
设矩阵A= 矩阵X满足AX+E=A2+X,试求矩阵X.
矩阵X满足AX+E=A2+X,试求矩阵X.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:由于AX+E=A2+X即(A—E)X=A2一E=(A-E)(A+E)因为A—E= 是可逆矩阵所以X=(A—E)-1(A—E)(A+E)=A+E=
是可逆矩阵所以X=(A—E)-1(A—E)(A+E)=A+E=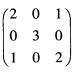
由于AX+E=A2+X,即(A—E)X=A2一E=(A-E)(A+E),因为A—E=是可逆矩阵,所以X=(A—E)-1(A—E)(A+E)=A+E=
相似问题
试证:由a1=(0 1 1)T a2=(1 0 1)T a3=(1 1 0)T所生成的向量空间就是R
试证:由a1=(0,1,1)T,a2=(1,0,1)T,a3=(1,1,0)T所生成的向量空间就是R3.请帮忙给出正确答案和分析,谢谢!
设A B∈Cn×n 0≤A请帮忙给出正确答案和分析 谢谢!
设A,B∈Cn×n,0≤A请帮忙给出正确答案和分析,谢谢!
已知矩阵A的伴随矩阵A*=diag(1 1 1 8) 且ABA-1=BA-1+3E 求B.请帮忙给出
已知矩阵A的伴随矩阵A*=diag(1,1,1,8),且ABA-1=BA-1+3E,求B.请帮忙给出正确答案和分析,谢谢!
构造一个相似于且不含零元的矩阵 它的谱半径是什么?它是非负矩阵吗?请帮忙给出正确答案和分析 谢谢!
构造一个相似于且不含零元的矩阵,它的谱半径是什么?它是非负矩阵吗?请帮忙给出正确答案和分析,谢谢!
设A=(αij)n×n≥0为不可约矩阵.则A不能有两个线性无关的非负特征向量.请帮忙给出正确答案和分
设A=(αij)n×n≥0为不可约矩阵.则A不能有两个线性无关的非负特征向量.请帮忙给出正确答案和分析,谢谢!












