设A B；都是实对称矩阵．证明：存在正交矩阵Q 使Q－1AQ=B的充要条件是A B的特征值全相等．请
设A，B；都是实对称矩阵．证明：存在正交矩阵Q，使Q－1AQ=B的充要条件是A，B的特征值全相等．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***101
2024-11-12 02:48:05
正确答案：必要性是显然的因为相似矩阵有相同的特征值．现证充分性．设λ1λ2…λn是A的特征值则它们也是B的特征值．于是存在正交矩阵X和Y使得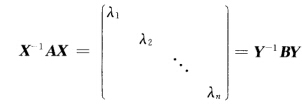
所以YX－1AXY－1=B令Q=XY－1则Q也是正交矩阵从而Q－1AQ=B．
必要性是显然的,因为相似矩阵有相同的特征值．现证充分性．设λ1,λ2,…,λn是A的特征值,则它们也是B的特征值．于是存在正交矩阵X和Y,使得所以YX－1AXY－1=B,令Q=XY－1,则Q也是正交矩阵,从而Q－1AQ=B．
相似问题
5局中甲至少胜3局的概率．请帮忙给出正确答案和分析 谢谢！
5局中甲至少胜3局的概率．请帮忙给出正确答案和分析，谢谢！
总体均值μ的区间估计中 下列正确的说法是( )．A．置信度1一a一定时 样本容量增加 则置信区间的长
总体均值μ的区间估计中，下列正确的说法是( )．A．置信度1一a一定时，样本容量增加，则置信区间的长度变长；B．置信度1—a一定时，样本容量增加，则置
设f(x1 x2 … xn)=XTAX是一实二次型 λ1 λ2 … λn是A的特征值 且λ1≤λ2≤
设f(x1，x2，…，xn)=XTAX是一实二次型，λ1，λ2，…，λn是A的特征值，且λ1≤λ2≤…≤λn证明：对若A=AH=A2∈Cm×n，r若A=AH=A2∈Cm×n，rank(a)=γ
设λ1 λ2是线性变换T的两个不同的特征值 ε1 ε2是分别属于λ1 λ2的特征向量 证明：ε1+ε
设λ1，λ2是线性变换T的两个不同的特征值，ε1，ε2是分别属于λ1，λ2的特征向量，证明：ε1+ε2不是T的特征向量． (2)证明：如果线性空间V中每一个非
设Hermite矩阵A非负定 证明：存在一个三角矩阵T 使得A=TTH．请帮忙给出正确答案和分析 谢
设Hermite矩阵A非负定，证明：存在一个三角矩阵T，使得A=TTH．请帮忙给出正确答案和分析，谢谢！
