设Hermite矩阵A非负定 证明：存在一个三角矩阵T 使得A=TTH．请帮忙给出正确答案和分析 谢
设Hermite矩阵A非负定，证明：存在一个三角矩阵T，使得A=TTH．
请帮忙给出正确答案和分析，谢谢！
参考解答
420***101
2024-11-12 02:28:28
正确答案：由于Hermite矩阵为正规矩阵由定理10知A=Udiag(λ1λ2…λn)UH．令P=diag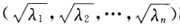
UH则有A=PHP．由定理1知P=UR．其中U是酉矩阵R是上三角复矩阵所以A=(UR)HUR=RHR．令T=RH则可得A=TTH．
由于Hermite矩阵为正规矩阵,由定理10知A=Udiag(λ1,λ2,…,λn)UH．令P=diagUH,则有A=PHP．由定理1知P=UR．其中U是酉矩阵,R是上三角复矩阵,所以A=(UR)HUR=RHR．令T=RH,则可得A=TTH．
相似问题
证明：正规矩阵A是幂零阵(A2=0)的充要条件是A=0．请帮忙给出正确答案和分析 谢谢！
证明：正规矩阵A是幂零阵(A2=0)的充要条件是A=0．请帮忙给出正确答案和分析，谢谢！
证明矩阵A=能够相似于对角矩阵 且A的特征值都是实数．请帮忙给出正确答案和分析 谢谢！
证明矩阵A=能够相似于对角矩阵，且A的特征值都是实数．请帮忙给出正确答案和分析，谢谢！
求单纯矩阵的谱分解式．请帮忙给出正确答案和分析 谢谢！
求单纯矩阵的谱分解式．请帮忙给出正确答案和分析，谢谢！
设A=(αij)m×n 定义实数1≤i≤m 1≤j≤n．证明：∥A∥GCm×n上的矩阵范数 且与向量
设A=(αij)m×n，定义实数1≤i≤m，1≤j≤n．证明：∥A∥GCm×n上的矩阵范数，且与向量的2－范数相容．请帮忙给出正确答案和分析，谢谢！
设A∈m×n可逆 B∈Cm×n 若对某种矩阵范数∥.∥ 有∥B∥
设A∈m×n可逆，B∈Cm×n，若对某种矩阵范数∥ ∥，有∥B∥<∥A－1∥ ，则A+B可逆．请帮忙给出正确答案和分析，谢谢！
