证明:一直线上的射影变换的集合构成群 其中△A>0的变换集合也构成群 问△A<0的变换集合是否也构成
证明:一直线上的射影变换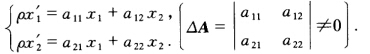 的集合构成群,其中△A>0的变换集合也构成群,问△A<0的变换集合是否也构成群?
的集合构成群,其中△A>0的变换集合也构成群,问△A<0的变换集合是否也构成群?
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:设: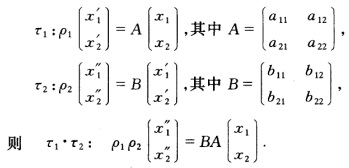 因|BA|=|B||A|≠0所以τ1.τ2仍为一维射影变换. 又设:
因|BA|=|B||A|≠0所以τ1.τ2仍为一维射影变换. 又设: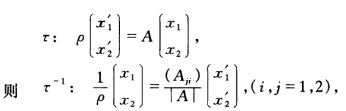 因|Aji|≠0所以τ-1仍为一维射影变换. 由此可得一直线上的射影变换的集合构成群.|A|<0的变换集合不构成群.
因|Aji|≠0所以τ-1仍为一维射影变换. 由此可得一直线上的射影变换的集合构成群.|A|<0的变换集合不构成群.
设:因|BA|=|B||A|≠0,所以τ1.τ2仍为一维射影变换.又设:因|Aji|≠0,所以τ-1仍为一维射影变换.由此可得一直线上的射影变换的集合构成群.|A|<0的变换集合不构成群.
相似问题
两个射影点列成透视的充要条件是_______.请帮忙给出正确答案和分析 谢谢!
两个射影点列成透视的充要条件是_______.请帮忙给出正确答案和分析,谢谢!
已知二级曲线的三条直线a b c及a b上的切点 试作出二级曲线的另一些直线 并作出c上的切点.请帮
已知二级曲线的三条直线a,b,c及a,b上的切点,试作出二级曲线的另一些直线,并作出c上的切点.请帮忙给出正确答案和分析,谢谢!
求由两个成射影对应λ′=的线束:χ1-λχ3=0和χ2-λ′χ3=0所构成的二阶曲线方程.请帮忙给出
求由两个成射影对应λ′=的线束:χ1-λχ3=0和χ2-λ′χ3=0所构成的二阶曲线方程.请帮忙给出正确答案和分析,谢谢!
求证:p q两直线关于非退化二阶曲线aijχiχj=0为共轭直线的充要条件是: 请帮忙给出正确答案和
求证:p、q两直线关于非退化二阶曲线aijχiχj=0为共轭直线的充要条件是: 请帮忙给出正确答案和分析,谢谢!
双曲线在仿射坐标系下(αχ+βy+γ)2+2(pχ+qy+γ)=0表示一抛物线.在仿射坐标系下(αχ
双曲线在仿射坐标系下(αχ+βy+γ)2+2(pχ+qy+γ)=0表示一抛物线.在仿射坐标系下(αχ+βy+γ)2+2(pχ+qy+γ)=0表示一抛物线.请帮忙给出












