求射影变换式 使直线上以0 1为坐标的点及无穷远点顺次对应以－1 0 1为坐标的点 并判定此射影变换
求射影变换式，使直线上以0，1为坐标的点及无穷远点顺次对应以－1，0，1为坐标的点，并判定此射影变换的类型．
请帮忙给出正确答案和分析，谢谢！
参考解答
481***102
2024-11-19 19:15:38
正确答案：设所求变换式为：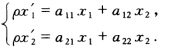
将(01)→(－11)(11)→(01)(10)→(11)代入上式得：
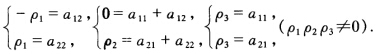解上列方程得：a11＝ρ3a12＝－ρ3a21＝ρ3a22＝ρ3代入所设变换式得所求变换式为：
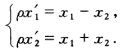求它的不变元素P(χ1χ2)→P(χ1χ2)得(1－ρ)2＋1＝0． 此方程无实数解故此变换无不变元素即为椭圆型射影变换．
设所求变换式为：将(0,1)→(－1,1),(1,1)→(0,1),(1,0)→(1,1)代入上式得：解上列方程得：a11＝ρ3,a12＝－ρ3,a21＝ρ3,a22＝ρ3,代入所设变换式,得所求变换式为：求它的不变元素P(χ1,χ2)→P(χ1,χ2),得(1－ρ)2＋1＝0．此方程无实数解,故此变换无不变元素,即为椭圆型射影变换．
相似问题
求下列对合的自对应点的坐标：求射影变换 使直线χ1＋χ2－6χ3＝0 χ1＋χ2＋6χ3＝0 χ1－
求下列对合的自对应点的坐标：求射影变换，使直线χ1＋χ2－6χ3＝0，χ1＋χ2＋6χ3＝0，χ1－χ2＋χ3＝0分别变成χ1＝0求射影变换，使直线χ1＋χ2－6
求直线z到自身的射影变换式 使P1(0) P2(1) P∞分别对应点P′(1) P∞ P′2(0)．
求直线z到自身的射影变换式，使P1(0)，P2(1)，P∞分别对应点P′(1)，P∞，P′2(0)．请帮忙给出正确答案和分析，谢谢！
已知射影坐标变换式：设以0 2 －2为参数的点分别对应以 －2为参数的点 求射影变换式．设以0 2
已知射影坐标变换式：设以0，2，－2为参数的点分别对应以，－2为参数的点，求射影变换式．设以0，2，－2为参数的点分别对应以，－2为参数的点，求射影变
已知直线l1 l3 l4的方程分别为：2χ1＋χ2－χ3＝0 χ1－χ2＋χ3＝0 χ1＝0 且(l
已知直线l1，l3，l4的方程分别为：2χ1＋χ2－χ3＝0，χ1－χ2＋χ3＝0，χ1＝0，且(l1l2，l3l4)＝－设a、b、c是通过点P的设a、b、c是通过点P的四条不同
已知直线l1 l3 l4的方程分别为：2χ1＋χ2－χ3＝0 χ1－χ2＋χ3＝0 χ1＝0 且(l
已知直线l1，l3，l4的方程分别为：2χ1＋χ2－χ3＝0，χ1－χ2＋χ3＝0，χ1＝0，且(l1l2，l3l4)＝－已知四直线： l已知四直线： l1：y＝k1χ＋b1，
