设P1 P2 P3 P4 P5 P6是六个不同的共线点 求证：如果(P1P2 P3p4)＝(P2P3
设P1，P2，P3，P4，P5，P6是六个不同的共线点，求证：如果(P1P2，P3p4)＝(P2P3，P4P1)，则(P1P3，P2P4)＝－1．
请帮忙给出正确答案和分析，谢谢！
参考解答
463***102
2024-11-19 19:25:39
正确答案：(P1P3P2P4) ＝1－(P1P2P3P4) ＝1－(P2P3P4P1) ＝(P1P3P4P2) ＝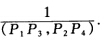
． 所以(P1P3P2P4)2＝1 因为P1、P2、P3、P4是不同的点所以(P1P3P2P4)＝－1．
(P1P3,P2P4)＝1－(P1P2,P3P4)＝1－(P2P3,P4P1)＝(P1P3,P4P2)＝．所以(P1P3,P2P4)2＝1因为P1、P2、P3、P4是不同的点,所以(P1P3,P2P4)＝－1．
相似问题
求射影变换式 使直线上以0 1为坐标的点及无穷远点顺次对应以－1 0 1为坐标的点 并判定此射影变换
求射影变换式，使直线上以0，1为坐标的点及无穷远点顺次对应以－1，0，1为坐标的点，并判定此射影变换的类型．请帮忙给出正确答案和分析，谢谢！
求下列对合的自对应点的坐标：求射影变换 使直线χ1＋χ2－6χ3＝0 χ1＋χ2＋6χ3＝0 χ1－
求下列对合的自对应点的坐标：求射影变换，使直线χ1＋χ2－6χ3＝0，χ1＋χ2＋6χ3＝0，χ1－χ2＋χ3＝0分别变成χ1＝0求射影变换，使直线χ1＋χ2－6
求直线z到自身的射影变换式 使P1(0) P2(1) P∞分别对应点P′(1) P∞ P′2(0)．
求直线z到自身的射影变换式，使P1(0)，P2(1)，P∞分别对应点P′(1)，P∞，P′2(0)．请帮忙给出正确答案和分析，谢谢！
已知射影坐标变换式：设以0 2 －2为参数的点分别对应以 －2为参数的点 求射影变换式．设以0 2
已知射影坐标变换式：设以0，2，－2为参数的点分别对应以，－2为参数的点，求射影变换式．设以0，2，－2为参数的点分别对应以，－2为参数的点，求射影变
已知直线l1 l3 l4的方程分别为：2χ1＋χ2－χ3＝0 χ1－χ2＋χ3＝0 χ1＝0 且(l
已知直线l1，l3，l4的方程分别为：2χ1＋χ2－χ3＝0，χ1－χ2＋χ3＝0，χ1＝0，且(l1l2，l3l4)＝－设a、b、c是通过点P的设a、b、c是通过点P的四条不同
