试用作图方法 分别构作双曲型射影变换 抛物型射影变换 椭圆型射影变换．请帮忙给出正确答案和分析 谢谢

正确答案：如图2—3—22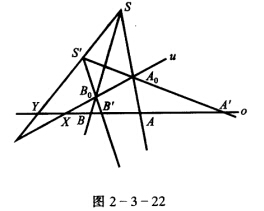． 二直线ou二点SS′不在o、u上分别以S、S′为中心将u上的点A₀、B₀、C₀、…投射到o上即 D(ABC…)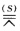(A₀B₀C₀…) u(A₀B₀C₀…)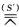(A′B′C′…)． 这个射影变换是双曲型的两个自对应点是o与u的交点Xo与SS′的交点Y如果SS′X三点共线则得抛物型的． 如图2—3—23以S为中心的线束将其按确定方向旋转同一角度φ则得另一个以S为中心的线束这两个线束成射影对应但没有自对应直线用同一直线S截两个线束得同底二点列成射影对应也没有自对应点因此是椭圆型射影变换．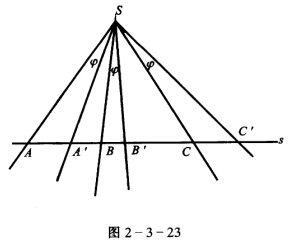
如图2—3—22．二直线o,u,二点S,S′不在o、u上,分别以S、S′为中心将u上的点A0、B0、C0、…投射到o上,即D(A,B,C,…)(A0,B0,C0,…),u(A0,B0,C0,…)(A′,B′,C′,…)．这个射影变换是双曲型的,两个自对应点是o与u的交点X,o与SS′的交点Y,如果S,S′,X三点共线,则得抛物型的．如图2—3—23,以S为中心的线束,将其按确定方向旋转同一角度φ,则得另一个以S为中心的线束,这两个线束成射影对应,但没有自对应直线,用同一直线S截两个线束得同底二点列成射影对应,也没有自对应点,因此是椭圆型射影变换．