从若f(z)在周线C内部除有一个一阶级点外解析 且连续到C 在C上｜f(z)｜=1．证明 f(z)=
从若f(z)在周线C内部除有一个一阶级点外解析，且连续到C，在C上｜f(z)｜=1．证明 f(z)=a (｜a｜＞1
若f(z)在周线C内部除有一个一阶级点外解析，且连续到C，在C上｜f(z)｜=1．证明 f(z)=a (｜a｜＞1) 在C内部恰好有一个根．
请帮忙给出正确答案和分析，谢谢！
参考解答
481***102
2024-11-21 00:34:52
正确答案：设f(z)一a在C的内部的零点个数为N下证N=1． 由于f(z)在C的内部只有一个极点故f(z)一a在C内的极点个数为1． 依辐角原理有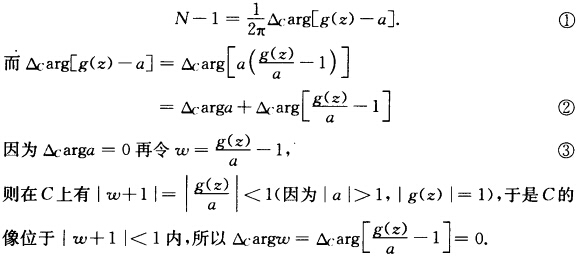 
将此结果与③式代入②得 △carg[f(z)一a=0． 再由①式得N=1．
设f(z)一a在C的内部的零点个数为N,下证N=1．由于f(z)在C的内部只有一个极点,故f(z)一a在C内的极点个数为1．依辐角原理有将此结果与③式代入②得△carg[f(z)一a=0．再由①式得N=1．
相似问题
设D是周线C的内部 f(z)在闭域=D+C上解析．试证：在D内不可能存在一点z0使 ｜f(z)｜＜｜
设D是周线C的内部，f(z)在闭域=D+C上解析．试证：在D内不可能存在一点z0使 ｜f(z)｜＜｜f(z0)｜ (z∈C)．请帮忙给出正确答案和分析，谢谢！
证明：函数z－2是函数 证明 f(z)==z＋z2＋z6＋…＋zn!＋… 以单位圆周｜z｜=1为自然
证明：函数z－2是函数 证明 f(z)==z＋z2＋z6＋…＋zn!＋… 以单位圆周｜z｜=1为自然边界．证明 f(z)==z+z2+z6+…+zn!+… 以单位圆周｜z｜=1为自然边
如果单叶解析函数w=f(z)把z平面上可求面积的区域D共形映射成w平面上的区域G 试证G的面积 A=
如果单叶解析函数w=f(z)把z平面上可求面积的区域D共形映射成w平面上的区域G，试证G的面积 A=｜f(z)｜2dxdy，(z=x+iy)．请帮忙给出正确答案和分析，谢谢！
设函数w=f(z)在｜z｜＜1内解析 且是将｜z｜＜1共形映射成｜w｜＜1的分式线性变换．试证 问线
设函数w=f(z)在｜z｜＜1内解析，且是将｜z｜＜1共形映射成｜w｜＜1的分式线性变换．试证 问线性变换w=将闭问线性变换w=将闭单位圆｜z｜≤1映成w平面上的
将下列函数在指定环域内展为洛朗级数． 将下列各函数在指定点的去心邻域内展成洛朗级数 并指出其将下列各
将下列函数在指定环域内展为洛朗级数． 将下列各函数在指定点的去心邻域内展成洛朗级数，并指出其将下列各函数在指定点的去心邻域内展成洛朗级数，并指
